Запишем основные виды уравнений прямой на плоскости.
1. Уравнение прямой, проходящей через данную точку 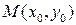 перпендикулярно данному ненулевому вектору
перпендикулярно данному ненулевому вектору
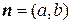 :
: 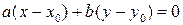 . Вектор
. Вектор 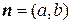 называется вектором нормали (нормальным вектором) этой прямой.
называется вектором нормали (нормальным вектором) этой прямой.
2. Общее уравнение прямой: 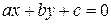 , где
, где 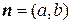 –нормальный вектор прямой.
–нормальный вектор прямой.
3. Уравнение прямой, проходящей через данную точку 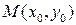 параллельно данному вектору
параллельно данному вектору 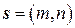 :
: 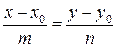 , где вектор
, где вектор 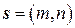 –направляющий вектор, уравнение называют каноническим.
–направляющий вектор, уравнение называют каноническим.
4. Параметрические уравнения прямой: 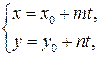 где
где 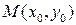 – точка, принадлежащая прямой. Параметрическое уравнение прямой в векторной форме:
– точка, принадлежащая прямой. Параметрическое уравнение прямой в векторной форме: 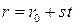 , где
, где 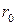 – радиус-вектор точки
– радиус-вектор точки 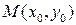 , а
, а 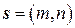 – направляющий вектор прямой.
– направляющий вектор прямой.
5. Уравнение прямой, проходящей через две данные точки 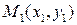 и
и 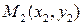 :
: 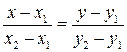 . Другая запись этого уравнения:
. Другая запись этого уравнения: 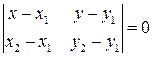 .
.
6. Уравнение прямой с угловым коэффициентом: 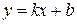 ,
, 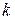 – угловой коэффициент прямой (
– угловой коэффициент прямой (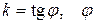 – угол между положительной полуосью
– угол между положительной полуосью 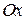 и прямой),
и прямой), 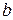 – ордината точки пересечения прямой с осью
– ордината точки пересечения прямой с осью 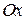 .
.
7. Уравнение прямой в отрезках: 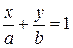 , где числа
, где числа 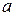 и
и 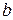 равны величинам отрезков, отсекаемых данной прямой на осях
равны величинам отрезков, отсекаемых данной прямой на осях 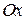 и
и 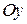 .
.
Расстояние 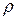 от точки
от точки 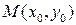 до прямой
до прямой 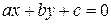 вычисляется по формуле
вычисляется по формуле 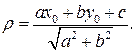
Если 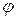 - угол между прямыми
- угол между прямыми 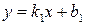 и
и 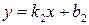 то
то 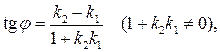
 где стрелка означает, что
где стрелка означает, что 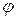 получается поворотом первой прямой ко второй против часовой стрелки.
получается поворотом первой прямой ко второй против часовой стрелки.
Пусть прямые 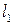 и
и 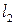 заданы своими общими уравнениями:
заданы своими общими уравнениями: 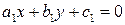 ,
, 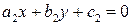 . Тогда:
. Тогда:
a) 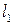 и
и 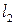 пересекаются, если и только если
пересекаются, если и только если 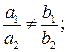
b) 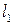 и
и 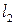 параллельны, если и только если
параллельны, если и только если 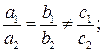
c) 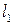 и
и 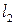 совпадают, если и только если
совпадают, если и только если 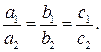
Пусть прямые 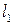 и
и 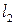 заданы уравнениями с угловым коэффициентами:
заданы уравнениями с угловым коэффициентами: 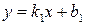
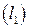 и
и 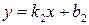
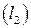 . Тогда:
. Тогда:
a) 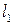 и
и 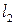 перпендикулярны в том и только том случае, когда
перпендикулярны в том и только том случае, когда 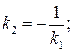
b) 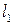 и
и 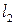 параллельны в том и только том случае, когда
параллельны в том и только том случае, когда 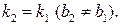
 2015-04-01
2015-04-01 1379
1379
