Пример 1. Даны координаты вершин треугольника АВС: 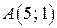 ,
, 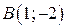 ,
, 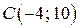 .Найти: 1) длину стороны ВС; 2) уравнение стороны ВС; 3) уравнение высоты, проведенной из вершины А; 4) длину высоты, проведенной из вершины А; 5) уравнение биссектрисы внутреннего угла
.Найти: 1) длину стороны ВС; 2) уравнение стороны ВС; 3) уравнение высоты, проведенной из вершины А; 4) длину высоты, проведенной из вершины А; 5) уравнение биссектрисы внутреннего угла 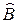 ; 6) угол
; 6) угол 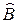 в радианах с точностью до 0.01.
в радианах с точностью до 0.01.
Решение.
1). Воспользовавшись формулой: 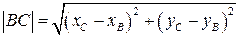 , получим
, получим
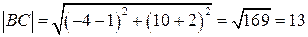 . Ответ:
. Ответ: 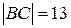 .
.
2) Воспользовавшись уравнением прямой, проходящей через две точки: 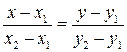 получим уравнение стороны ВС:
получим уравнение стороны ВС: 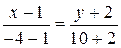 ,
, 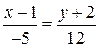 ,
, 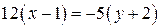 ,
, 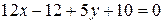 ,
, 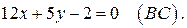 Ответ:
Ответ: 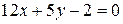
3) Высота АН перпендикулярна стороне ВС, поэтому их угловые коэффициенты 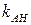 и
и 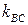 удовлетворяют условию:
удовлетворяют условию: 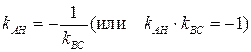 . Из уравнения прямой ВС следует, что
. Из уравнения прямой ВС следует, что 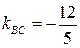 , тогда
, тогда 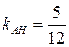 .
.
Уравнение прямой, проходящей через точку 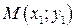 с угловым коэффициентом k имеет вид:
с угловым коэффициентом k имеет вид: 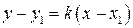 . Напишем уравнение прямой, проходящей через данную точку
. Напишем уравнение прямой, проходящей через данную точку 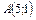 с угловым коэффициентом
с угловым коэффициентом 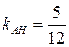 :
:
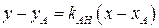 ,
, 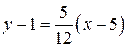 ,
, 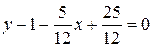 ,
, 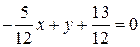 ,
, 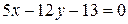
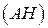 . Ответ:
. Ответ: 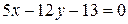 .
.
4) Длину высоты АН вычисляем как расстояние от точки А до прямой ВС по формуле: 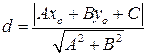 ; где
; где 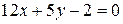
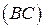 .
.
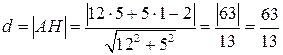 ;
; 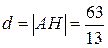 . Ответ:
. Ответ: 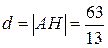 .
.
5) Пусть D – точка пересечения биссектрисы со стороной АС. Из свойства биссектрисы внутреннего угла треугольника следует, что 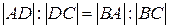 . Но
. Но 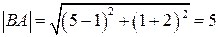 ,
,
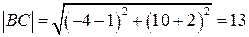 .
.
Следовательно, 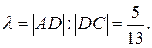 Так как известно, в котором точка D делит отрезок АС, то координаты точки D определяются по формулам:
Так как известно, в котором точка D делит отрезок АС, то координаты точки D определяются по формулам:
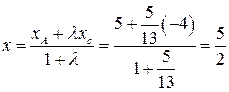 .
. 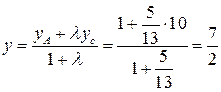 , т.е.
, т.е. 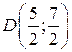 .
.
Задача сводится к составлению прямой, проходящей через точки В и D.
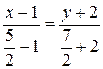 ,
, 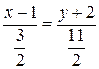 ,
, 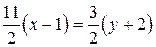 ,
, 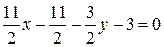 ,
,
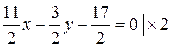 ,
, 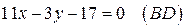 .
.
Ответ: 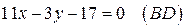 .
.
6) Найдем координаты векторов 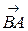 и
и 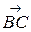 :
: 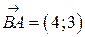 ,
, 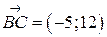 .
.
Скалярное произведение векторов 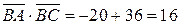 . Тогда
. Тогда 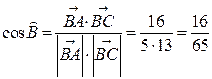 . Ответ:
. Ответ: 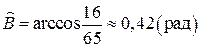 .
.
 2015-04-01
2015-04-01 18530
18530
