Определение 1. Линейной комбинацией векторов  ,
,  ,
, 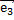 называется сумма произведений этих векторов на какие-нибудь числа
называется сумма произведений этих векторов на какие-нибудь числа 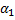 ,
, 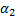 ,
, 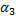 :
: 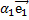 +
+ 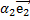 +
+ 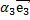 .
.
Определение 2. Векторным базисом в данной плоскости называется любая пара неколлинеарных векторов  и
и  этой плоскости.
этой плоскости.
Вектор  называют при этом первым базисным вектором, вектор
называют при этом первым базисным вектором, вектор  -вторым.
-вторым.
Справедлива следующая теорема.
Теорема 1. Если базис  ,
,  – векторный базис в плоскости, тогда любой вектор
– векторный базис в плоскости, тогда любой вектор  этой плоскости может быть представлен, и притом единственным образом, в виде линейной комбинации базисных векторов
этой плоскости может быть представлен, и притом единственным образом, в виде линейной комбинации базисных векторов 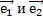 :
:  = х
= х  +у
+у  . (*)
. (*)
Определение 3. Равенство(*) называют разложением вектора  по базису
по базису  ,
,  , а числа х и у – координатами вектора
, а числа х и у – координатами вектора  в базисе
в базисе  ,
,  (или относительно базиса
(или относительно базиса  ,
,  ). Если заранее ясно, о каком базисе идет речь, то пишут кратко:
). Если заранее ясно, о каком базисе идет речь, то пишут кратко:  ={x,y}. Из определения координат вектора относительно базиса следует, что равные векторы имеют соответственно равные координаты.
={x,y}. Из определения координат вектора относительно базиса следует, что равные векторы имеют соответственно равные координаты.
Два и более векторов в пространстве называются компланарными, если они параллельны одной и той же плоскости или лежат в этой плоскости.
Определение 4. Векторным базисом в пространстве называют любые три вектора  ,
,  ,
, 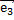 .
.
Вектор  называют при этом первым базисным вектором,
называют при этом первым базисным вектором,  - вторым,
- вторым, 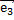 -третьим.
-третьим.
Замечание. 1. Три вектора  = {
= { 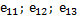 },
},  = {
= { 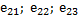 } и
} и 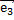 = {
= { 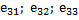 } образуют базис пространства, если определитель, составленный из их координат, отличен от нуля:
} образуют базис пространства, если определитель, составленный из их координат, отличен от нуля:
 .
.
2. Основные положения теории определителей и способы их вычисления рассмотрены в модуле 1 «линейная алгебра».
Теорема 2. Пусть  ,
,  ,
, 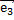 - векторный базис в пространстве. Тогда любой вектор
- векторный базис в пространстве. Тогда любой вектор  в пространстве может быть представлен, и притом единственным образом, в виде линейной комбинации базисных векторов
в пространстве может быть представлен, и притом единственным образом, в виде линейной комбинации базисных векторов  ,
,  и
и 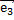 :
:
 = х
= х  +у
+у  +z
+z 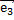 . (**)
. (**)
Определение 5. Равенство (**) называют разложением вектора  по базису
по базису  ,
,  ,
, 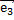 , а числа x,y,z–координатами (компонентами) вектора
, а числа x,y,z–координатами (компонентами) вектора  в базисе
в базисе  ,
,  ,
, 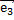 .
.
Если заранее ясно, о каком базисе идет речь, то пишут кратко:  = {x,y,z}.
= {x,y,z}.
Определение 6. Базис  ,
,  ,
, 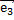 называется ортонормированным, если векторы
называется ортонормированным, если векторы  ,
,  ,
, 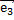 попарно перпендикулярны и имеют единичную длину. В этом случае приняты обозначения
попарно перпендикулярны и имеют единичную длину. В этом случае приняты обозначения 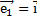 ,
, 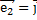 ,
, 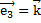 .
.
 2015-04-01
2015-04-01 6249
6249
