Изучение теоретических основ стоимости денег во времени необходимо начать с определения различия между простым и сложным начислением процентов. В таблице 1 проиллюстрировано накопление денежной суммы с применением простого и сложного начисления процентов.
Таблица 1 – Пример простого и сложного начисления процентов
(10% годовых)
| Дата | Простое начисление процентов | Начисление по сложному проценту | ||||
| Сумма | Сумма | |||||
| начальная | процентов | конечная | начальная | процентов | конечная | |
| 01.01.2011 | – | – | – | – | ||
| 01.01.2012 | ||||||
| 01.01.2013 | ||||||
| 01.01.2014 | 12,1 | 133,1 | ||||
| 01.01.2015 | 133,1 | 13,31 | 146,41 |
При сложном начислении процентов в накоплении участвует как первоначальная сумма вклада, так и прирост, полученный в предыдущем периоде.
Расчёт стоимости денег во времени при использовании сложного процента описывается шестью функциями денежной единицы (сложного процента), которые составляют три пары взаимообратных функций (рисунок 1).
 | |||
 |
| I | II | III | IV | V | VI |
| PV i n | PMT i n | FV i n | FV i n | PMT i n | PV i n |
| FV | FV | PMT | PV | PV | PMT |
Рисунок 1 – Шесть функций сложного процента:
три пары взаимообратных функций
Для расчёта стоимости денег во времени можно использовать таблицы сложного процента, математические выражения (таблица 2) или финансовый калькулятор.
В таблице 2 представлены формулы для расчёта. В расчётах используются следующие показатели:
1) PV – текущая стоимость;
2) FV – будущая стоимость;
3) PMT – равновеликий периодический платёж (аннуитет);
4) i – ставка дисконта;
5) n – период времени;
6) К – значение колонки в таблице сложного процента.
Таблица 2 – Функции сложного процента
| Наименование функции | Основная формула | Формула для использования таблиц сложного процента |
| Сумма единицы по сложному проценту | 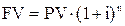 | 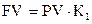 , , 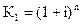 |
| Будущая стоимость обычного аннуитета единицы за период | 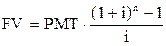 | 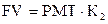 , , 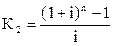 |
| Фактор фонда возмещения капитала | 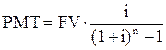 | 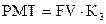 , , 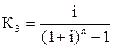 |
| Текущая стоимость реверсии единицы за период | 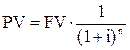 | 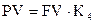 , , 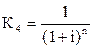 |
| Текущая стоимость обычного аннуитета единицы за период | 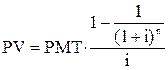 | 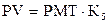 , , 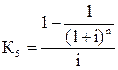 |
| Взнос на амортизацию денежной единицы | 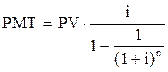 | 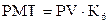 , , 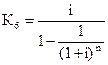 |
Например, необходимо найти размер периодического равновеликого платежа в счёт погашения 1 тыс. руб., предоставленной на 2 года под 15% годовых.
Дано: PV = 1 тыс. руб.; n = 2 года; i = 15%.
Найти: PMT –?
Решение:
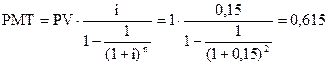 тыс. руб.
тыс. руб.
Ответ: 0,615 тыс. руб.
Решим предыдущую задачу с использованием таблиц сложного процента.
Дано: PV = 1 тыс. руб.; n = 2 года; i = 15%.
Найти: PMT –?
Решение:
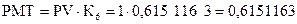 »0,615 тыс. руб.
»0,615 тыс. руб.
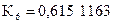 (значение в таблице 3 на пересечении 2 года и 6 функции при 15% ежегодном начислении процентов).
(значение в таблице 3 на пересечении 2 года и 6 функции при 15% ежегодном начислении процентов).
Таблица 3 – Таблица шести функций денежной единицы
| Годы | Накопленная сумма денежной единицы | Накопление денежной единицы за период | Фактор фонда возмещения | Текущая стоимость денежной единицы | Текущая стоимость аннуитета | Взнос на амортизацию денежной единицы |
| Ежегодное начисление, 15 % | ||||||
| 1,150 000 | 1,000 000 | 1,000 000 0 | 0,869 565 | 0,869 57 | 1,150 000 0 | |
| 1,322 500 | 2,150 000 | 0,465 116 3 | 0,756 144 | 1,625 71 | 0,615 116 3 | |
| 1,520 875 | 3,472 500 | 0,287 977 0 | 0,657 516 | 2,283 23 | 0,437 977 0 | |
| 1,749 006 | 4,993 375 | 0,200 265 4 | 0,571 753 | 2,854 98 | 0,350 265 4 |
Ответ: 0,615 тыс. руб.
Применение финансового калькулятора «Casio FС-100V»
1. Включить калькулятор.
2. Войти в систему финансовых расчётов путём нажатия клавиши
| CDMP |
3. Откроется меню ввода величин
| Compund Int. | |
| Set | : End |
| n | =0 |
| I% | =0 |
| PV | =0 |
| PMT | =0 |
| FV | =0 |
| P/Y | =1 |
| C/Y | =1 |
| где Set | – | режим выбора даты оплаты (End – конец периода; Begin – начало периода); |
| P/Y | – | число платежей в год; |
| C/Y | – | число начислений сложного процента за год. |
4. Прокрутка меню (ввод значений) производится с помощью клавиш
| ß | и | Ý |
5. После ввода каждого известного значения необходимо нажать клавишу «да»
| ЕХЕ |
6. Если показатель не используется в расчёте, то он остаётся равным «0».
7. Вводите одно из известных значений PV, PMT или FV как отрицательную величину используя клавишу «–» (минус) перед значением.
8. Выберите величину, которую необходимо вычислить (установите курсор в строке) и нажмите клавишу
| SOLVE |
9. В строке искомого показателя появится рассчитанное значение.
Например, необходимо найти размер периодического равновеликого платежа в счёт погашения 1 тыс. руб., предоставленной на 2 года под 15% годовых
| Compund Int. | ||
| Set | : End | |
| n | =2 | |
| I% | =15 | |
| PV | =-1 | |
| PMT | =0 | После нажатия клавиши «SOLVE» появится результат «=0,615» |
| FV | =0 | |
| P/Y | =1 | |
| C/Y | =1 |
Если необходимо определить размер ежемесячного периодического равновеликого платежа в счёт погашения 1 тыс. руб., предоставленной на 2 года под 15% годовых, то ввод данных несколько изменится
| Compund Int. | ||
| Set | : End | |
| n | =2´12 | |
| I% | =15 | |
| PV | =-1 | |
| PMT | =0 | После нажатия клавиши «SOLVE» появится результат «=0,0484» |
| FV | =0 | |
| P/Y | =12 | |
| C/Y | =12 |
Для решения подобных задач можно использовать финансовые функции Excel (таблица 4).
Таблица 4 – Применение финансовых функций Excel
| Функция Excel | Рассчитываемый показатель | Функция сложного процента |
| БС | FV | 1, 2 |
| ПС | PV | 4, 5 |
| ПТЛ | PMT | 3, 6 |
| КПЕР | n | 1, 2, 3, 4, 5, 6 |
| СТАВКА | i, % |
Например, необходимо определить будущую стоимость первоначального вклада в размере 1 000 руб., предоставленного на 4 года под 12% при ежегодном начислении процентов.
Решение:
Воспользуемся функцией Excel «БС» − будущая стоимость. Занесём имеющиеся данные:
− Ставка=0,12 (i=12 %);
− Кпер=4 (n=4);
− Пс=-1 000 (PV=-1 000);
− Тип=0 (0 или 1 – указывает на тип платежа – обычный или авансовый).
Здесь также один из известных показателей (Бс, Пс или Плт) заносится со знаком «-» (минус).
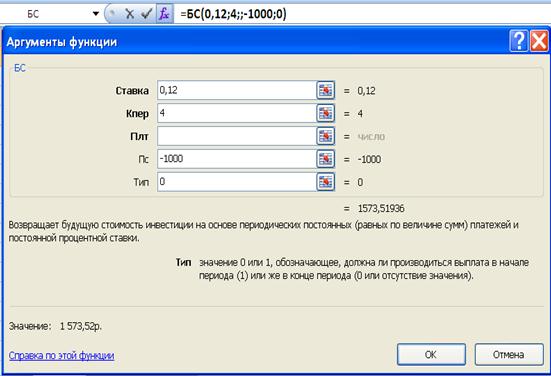
После занесения всех данных результат отображается на экране. В нашем случае БС=1 573,519 36 или 1 573,52 руб.
Ответ: 1 573,52 руб.
 2015-04-01
2015-04-01 1655
1655








