2015-04-01
31473
Общие сведения
Активными фильтрами называют электронные усилители, содержащие RC -цепи, с помощью которых усилителю придаются определенные избирательные свойства.
а
б
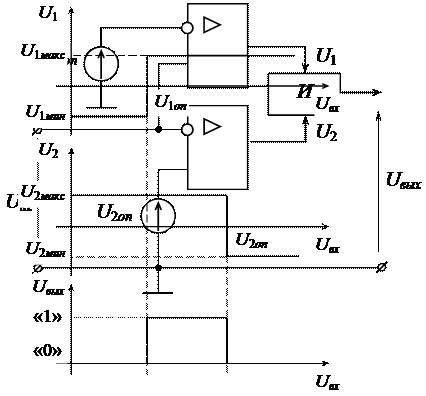
Рисунок 3.26 – Двухпороговый компаратор напряжения
Применение усилительных элементов выгодно отличает активные фильтры от фильтров на пассивных элементах.
К преимуществам активных фильтров в первую очередь следует отнести:
- способность усиливать сигнал, лежащий в полосе пропускания фильтра;
- возможность отказаться от применения таких нетехнологичных элементов, как катушки индуктивности, использование которых несовместимо с методами интегральной технологии;
- простота настройки;
- малые масса и объем, которые слабо зависят от полосы пропускания, что особенно важно при разработке устройств, работающих в низкочастотной области;
- простота каскадного включения при построении фильтров высоких порядков.
Вместе с тем активным фильтрам свойственны следующие недостатки, ограничивающие область их применения:
- невозможность использования в силовых цепях, например в качестве фильтров во вторичных источниках питания;
- необходимость использования дополнительного источника энергии, предназначенного для питания активных элементов усилителя;
- ограниченный частотный диапазон, определяемый собственными частотными свойствами используемых усилителей.
Несмотря на перечисленные недостатки, активные фильтры находят широкое практическое применение. Особый интерес представляют активные фильтры, выполненные на основе ОУ. Они позволяют получать стабильные и в тоже время недорогие частотно-избирательные цепи в диапазоне частот от 0 до 100 кГц. Применение активных фильтров на ОУ в области низких частот позволяет избавиться от громоздких конденсаторов и катушек индуктивности, которым, кроме всего прочего, присущи большие потери.
Основным параметром фильтра является его полоса пропускания – область частот, в пределах которой фильтр обладает малым ослаблением (затуханием). Как и в усилителях, она определяется по уровню уменьшения коэффициента усиления в 1,41 раза (на 3 дБ). Область частот, в пределах которой фильтр существенно ослабляет сигнал, называется полосой задержания (заграждения, подавления).
По характеру расположения полосы пропускания и полосы задержания активные фильтры, как и фильтры на пассивных элементах, подразделяются на:
- фильтры нижних частот (ФНЧ), пропускающие сигналы в диапазоне частот от w = 0 до w = w в (рисунок 3.27, а);
- фильтры верхних частот (ФВЧ), пропускающие сигналы с частотой от w = w н до w ® ¥ (рисунок 3.27, б);
- полосовые фильтры (ПФ), пропускающие сигналы в диапазоне частот от w н до w в (рисунок 3.27, в);
- режекторные (заградительные) фильтры, не пропускающие сигналы в узком диапазоне частот от w зн до w зв (рисунок 3.27, г).
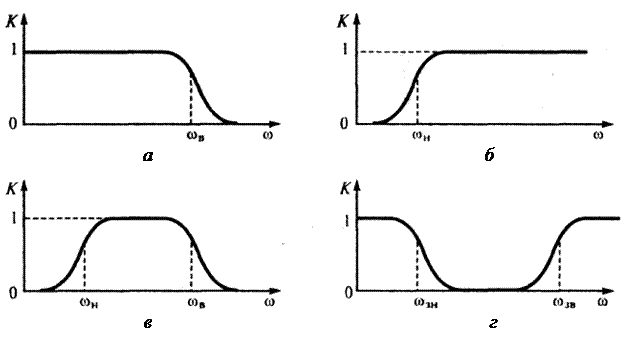
Рисунок 3.27 – АЧХ разных типов фильтров
Для решения конкретных задач по обработке сигналов в настоящее время разработано большое число различных схем активных фильтров. Наиболее известными из них являются фильтры Чебышева, Баттерворта и Бесселя. Основным различием этих фильтров является выбор математической функции для аппроксимации АЧХ фильтра.
Рассмотрим общие принципы применения ОУ с цепями частотно-зависимой ООС для формирования устройств с различными частотными свойствами.
Фильтры нижних и верхних частот
Простейшими активными фильтрами нижних и верхних частот первого порядка являются, соответственно, интегрирующий (рисунки 3.13, 3.14) и дифференцирующий (рисунки 3.16, 3.17) усилители. В них основным элементом, определяющим частотную характеристику усилителя, является конденсатор, включенный в цепь обратной связи.
Передаточные функции простейших фильтров представляют собой уравнения первого порядка, поэтому и фильтры называются фильтрами первого порядка. Наклон логарифмической АЧХ (ЛАЧХ) за пределами полосы пропускания у фильтров первого порядка составляет всего –20 дБ/дек, что свидетельствует о плохих избирательных свойствах таких фильтров.
Для улучшения избирательности нужно либо повышать порядок передаточной функции фильтра за счет введения дополнительных RC -цепей, либо последовательно включать несколько идентичных активных фильтров.
На практике наиболее часто в качестве фильтров используют ОУ с цепями ОС, работа которых описывается уравнениями второго порядка. При необходимости повысить избирательность системы несколько фильтров второго порядка включают последовательно (например, для получения ФНЧ четвертого порядка последовательно включают два ФНЧ второго порядка, для получения ФНЧ шестого порядка – три ФНЧ второго порядка и т. д.).
Активные фильтры низких и высоких частот второго порядка приведены на рисунке 3.28, а, б. У них, при соответствующем подборе номиналов резисторов и конденсаторов, спад ЛАЧХ за пределами полосы пропускания составляет 40 дБ/дек. Причем, как видно из рисунка 3.28, переход от фильтра нижних к фильтру верхних частот осуществляется заменой резисторов на конденсаторы, и наоборот.
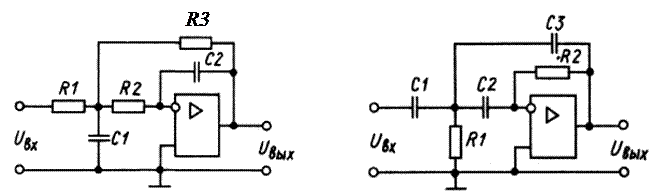
а б
Рисунок 3.28 – ФНЧ (а) и ФВЧ (б) второго порядка на операционном усилителе
Передаточная функция фильтра НЧ второго порядка описывается выражением
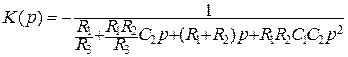, (3.38)
а фильтра ВЧ второго порядка – выражением
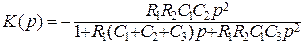. (3.39)
Частоты среза фильтров второго порядка соответственно равны:
- для ФНЧ
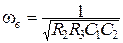; (3.40)
- для ФВЧ
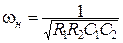. (3.41)
В последнее время широкое распространение получили активные ФНЧ и ФВЧ второго порядка, реализованные на повторителях напряжения (максимальное значение коэффициента усиления напряжения у таких фильтров в пределах полосы пропускания равно 1). Схемы названных фильтров показаны на рисунке 3.29, а (ФНЧ) и 3.29, б (ФВЧ).
а б
Рисунок 3.29 – ФНЧ (а) и ФВЧ (б) второго порядка на повторителях напряжения
Последовательность расчета элементов фильтров, выполненных на основе повторителей, состоит в следующем:
а) по графикам (рисунок 3.30) выбрать подходящую характеристику фильтра (с учетом требуемой избирательности) и определить число полюсов, требующееся для получения желаемого затухания;
б) из схем на повторителях выбрать подходящую схему фильтра (рисунок 3.29);
в) пользуясь данными таблицы 3.2, выполнить необходимый пересчет параметров элементов фильтра.
В таблице 3.2 даны значения емкостей (в фарадах) для схемы повторителя в зависимости от числа полюсов фильтра. При этом для получения фильтра, например, четвертого порядка, используют каскадное включение двух одинаковых повторителей, но элементы первого каскада рассчитывают как для фильтра с двумя полюсами, а второго каскада – как для фильтра с четырьмя полюсами.
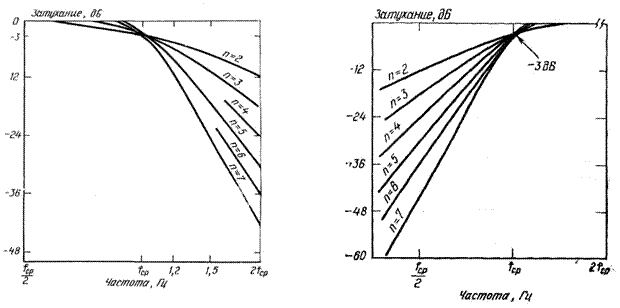
Рисунок 3.30 – Амплитудно-частотные характеристики ФНЧ (слева) и ФВЧ (справа) Баттерворта
Таблица 3.2 – Величины емкостей конденсаторов (фарад)
| Число полюсов | Фильтр Бесселя | Фильтр Баттерворта | ||
| C 1 | С 2 | C 1 | С 2 | |
| 0,9066 | 0,6799 | 1,414 | 0,7071 | |
| 0,7351 1,0120 | 0,6746 0,3900 | 1,082 2,613 | 0,9241 0,3825 | |
| 0,6352 0,7225 1,0730 | 0,6098 0,4835 0,2561 | 1,035 1,414 3,863 | 0,9660 0,7071 0,2588 | |
| 0,5673 0,6090 0,7257 1,1160 | 0,5539 0,4861 0,3590 0,1857 | 1,091 1,202 1,800 5,125 | 0,9809 0,8313 0,5557 0,1950 | |
| 0,5172 0,5412 0,5999 0,7326 1,1510 | 0,5092 0,4682 0,3896 0,2792 0,1437 | 1,012 1,122 1,414 2,202 6,389 | 0,9874 0,8908 0,7071 0,4540 0,1563 |
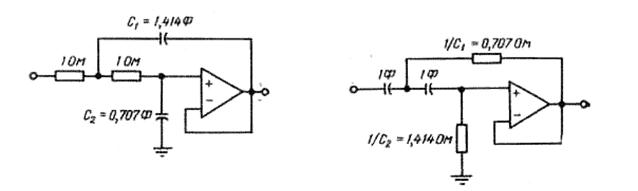
На рисунке 3.31 показана процедура расчета схем фильтров на повторителях на примере двухполюсных ФНЧ (слева) и ФВЧ (справа) Баттерворта с частотой среза fв = 1 кГц.
Величины компонентов, взятые из таблицы 3.2, для схемы ФНЧ нормированы для частоты 1 рад/с при сопротивлении резисторов 1 Ом и емкости конденсаторов в фарадах. Емкости конденсаторов фильтра пересчитываются по частоте делением величин емкостей, взятых из таблицы, на частоту среза в радианах (2p fв). Компоненты фильтра пересчитывают умножением величин сопротивлений на подходящий коэффициент (например, 104) и делением величин емкостей на тот же коэффициент. В результате получаем следующие значения параметров элементов ФНЧ: С 1 = 0,0225 мкФ, С 2 = 0,0112 мкФ, R 1 = R 2 = 10 кОм.
Величины компонентов, взятые из таблицы 3.2, для схемы ФВЧ нормированы для частоты 1 рад/с при емкости конденсаторов 1 Ф и сопротивлении резисторов в омах, обратных значениям емкостей. Емкости конденсаторов фильтра пересчитываются по частоте делением величин емкостей на частоту среза в радианах (2p fн). Компоненты фильтра пересчитывают умножением величин сопротивлений на подходящий коэффициент (например, 14,1 103) и делением величин емкостей на тот же коэффициент. В результате получаем следующие значения параметров элементов ФВЧ: С 1 = С 2 = 0,0113 мкФ, R 1 = 10 кОм, R 2 = 20 кОм.
Полосовой и режекторный фильтры
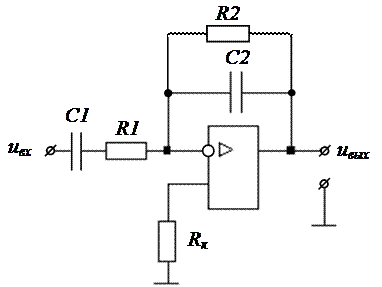
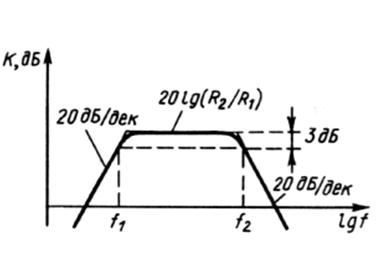
Простейший полосовой фильтр может быть получен посредством объединения фильтров нижних и верхних частот (например, интегратора и дифференциатора). Пример такой схемы показан на рисунке 3.32, а, а его логарифмическая АЧХ – на рисунке 3.32, б.
Частоты среза фильтра определяются из выражений:
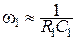, (3.42)
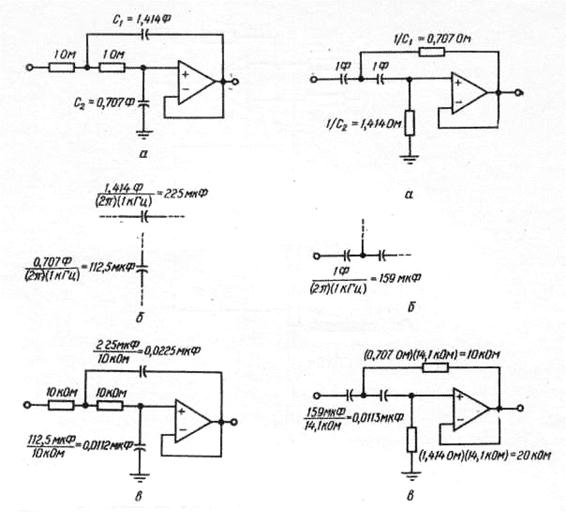
Рисунок 3.31 – Последовательность расчета ФНЧ (слева) и ФВЧ (справа)
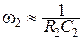. (3.43)
Для измерительной техники и техники обработки сигналов представляют интерес три типа схем ПФ:
- фильтр с многопетлевой обратной связью – применяется при величинах добротности до 10 и выгодно отличается от других схем тем, что имеет всего лишь один операционный усилитель;
- биквадратный резонатор – является более сложным электрическим фильтром, выполняемым на трех ОУ и обеспечивающим добротность до 200;
- коммутируемый фильтр – обеспечивает добротность до 1000, необходимую при селекции узкополосных сигналов.
а
б
Рисунок 3.32 – Схема и логарифмическая АЧХ полосового фильтра
Добротность Q во всех случаях определяется следующим отношением
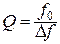, (3.44)
где f 0 – средняя частота полосы пропускания;
D f – ширина полосы пропускания на уровне –3 дБ (то есть на уровне 0,707 KUмакс).
АЧХ полосовых фильтров для различных значений Q приведены на рисунке 3.33.
 |
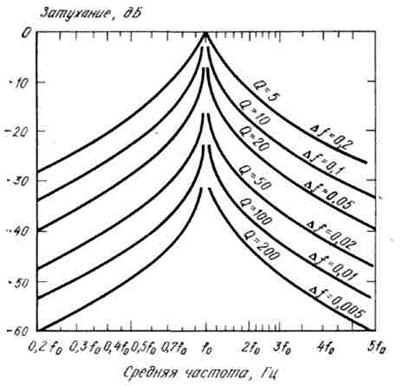Рисунок 3.33 – АЧХ полосовых фильтров при разных значениях добротности
На рисунке 3.34 показана схема полосового фильтра с многопетлевой ОС (ПФМОС) и вид его АЧХ.
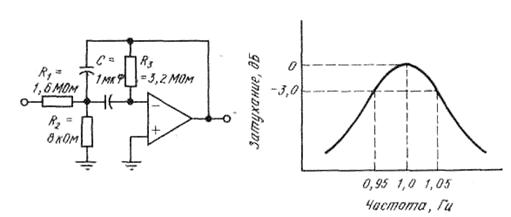
Рисунок 3.34 – Полосовой фильтр с многопетлевой обратной связью
Сопротивления резисторов R1, R2 и R3 ПФМОС при заданной емкости конденсаторов С = 1 мкФ, выбирают с учетом требуемой добротности Q и средней частоты f 0 по формулам:
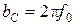, (3.45)
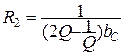, (3.46)
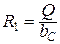, (3.47)
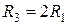. (3.48)
Чтобы получить максимальную стабильность фильтра, расчет ведется для единичного усиления на частоте f 0.
Полосовой фильтр второго порядка может быть выполнен по схеме, показанной на рисунке 3.45.
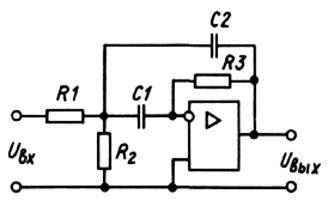
Рисунок 3.45 – Полосовой фильтр второго порядка
Квазирезонансная частота ПФ второго порядка (на которой коэффициент передачи фильтра максимален) может быть найдена из выражения
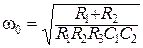. (3.49)
Режекторный фильтр может быть получен на основе схемы ПФМОС, если к ее выходу подключить неинвертирующий сумматор (рисунок 3.46). В такой схеме выделенный на частоте f 0 сигнал c выхода инвертирующего ПФМОС, коэффициент усиления напряжения которого равен единице, поступает на один из входов неинвертирующего сумматора. Входной широкополосный сигнал поступает на второй вход сумматора также без усиления и без изменения фазы. В результате сложения двух сигналов в противофазе происходит подавление сигнала в области частоты режекции f 0, то есть обеспечивается требуемый вид АЧХ для режекторного фильтра.
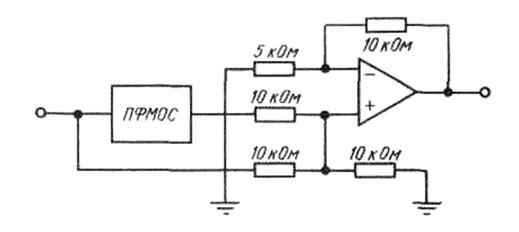
Рисунок 3.46 – Режекторный фильтр на основе схемы ПФМОС
Нужно отметить, что выше рассмотрены только отдельные примеры построения схем активных фильтров. На практике широко применяются также схемы, основу которых составляют мост Вина или двойной Т-мост.
