Используя операции сложения и умножения комплексных чисел, запишем комплексное число 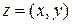 в виде:
в виде:
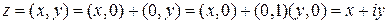 .
.
Эта форма записи комплексного числа называется алгебраической формой.
Комплексные числа, записанные в алгебраической форме можно складывать и умножать как обычные двучлены, учитывая, что 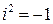 .
.
Пример. 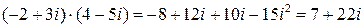 .
.
Определение. Два комплексных числа 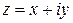 и
и 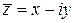 , которые отличаются знаком у мнимой части, называют комплексно сопряженными числами.
, которые отличаются знаком у мнимой части, называют комплексно сопряженными числами.
Подчеркнем, что 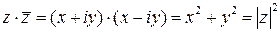 .
.
Операцию деления комплексных чисел, записанных в алгебраической форме, можно определить с помощью операции умножения. А именно, чтобы вычислить значение 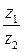 надо числитель и знаменатель дроби умножить на число, сопряженное знаменателю:
надо числитель и знаменатель дроби умножить на число, сопряженное знаменателю:
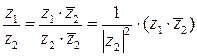 .
.
Пример. 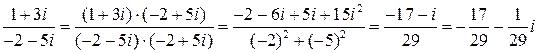 .
.
Используя понятие модуля и аргумента комплексного числа можно записать:
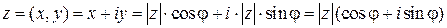 .
.
Эту форму записи называют тригонометрической формой записи комплексного числа.
Числа, записанные в тригонометрической форме, удобно умножать и делить, используя свойства модуля и аргумента.
Введем обозначение 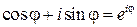 (позже мы увидим, что введенный здесь формально символ
(позже мы увидим, что введенный здесь формально символ 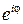 есть не что иное, как
есть не что иное, как 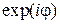 ). Тогда получим показательную форму записи комплексного числа:
). Тогда получим показательную форму записи комплексного числа:
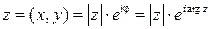 .
.
Таким образом, всякое комплексное число 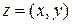 можно записать в трех формах:
можно записать в трех формах:
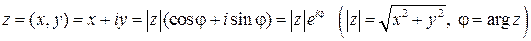 .
.
В силу указанных свойств модуля и аргумента, операции умножения и деления комплексных чисел удобнее выполнять, если эти числа записаны в тригонометрической или показательной форме.
Пример. Записать комплексное число 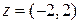 в трех формах записи.
в трех формах записи.
Решение. 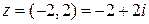 - алгебраическая форма записи.
- алгебраическая форма записи. 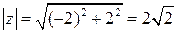 ,
, 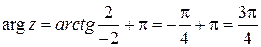 ,
,
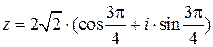 - тригонометрическая форма записи,
- тригонометрическая форма записи,
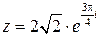 - показательная форма записи.
- показательная форма записи.
Пример. Вычислить 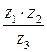 , если
, если 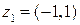 ,
, 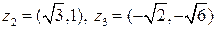 .
.
Решение. Запишем данные комплексные числа в показательной форме. 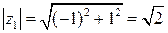 ,
, 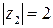 ,
, 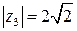 .
. 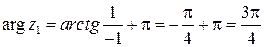 ,
, 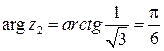 ,
, 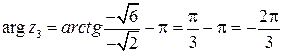 . Тогда
. Тогда 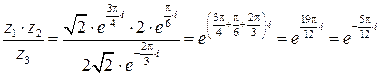 .
.
 2015-04-01
2015-04-01 4294
4294
