2015-04-01
1128
Если при вычислении предела функции возникает неопределенность вида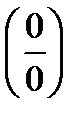 
или вида 
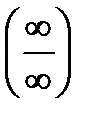, и никакой из существующих приемов ее раскрытия не работает, на помощь придет правило Лопиталя. Под правилом Лопиталя понимают прием раскрытия неопределенностей вида 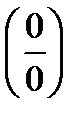или .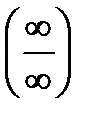
Теорема (правило Лопиталя). Для вычисления предела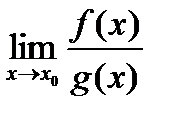 
, где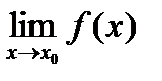 
= 
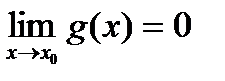, достаточно найти предел отношения производных данных функций (если он существует), т.е. = 
.
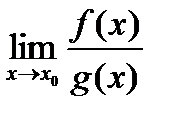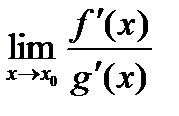Замечание. 1. Правило Лопиталя справедливо также для случаев
· неопределенности вида 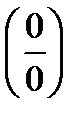при х →∞;
· неопределенности вида 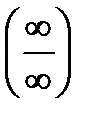при х → хо и х →∞.
2. Правило Лопиталя может быть применено последовательно несколько раз для раскрытия неопределенностей вида 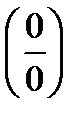или .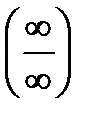
Рассмотрим примеры нахождения пределов функций с использованием правила Лопиталя.
Пример 1. Вычислите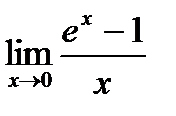 
.
Решение. Поскольку в примере встречается неопределенность вида 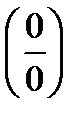, можно применить правило Лопиталя:
= 
= 
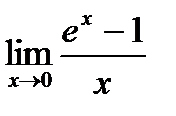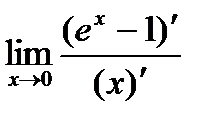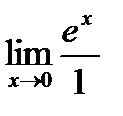= е0 =1.
Ответ: 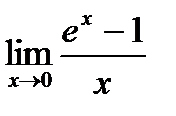=1.
Пример 2. Вычислите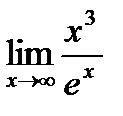 
.
Решение. Поскольку в примере рассматривается неопределенность вида 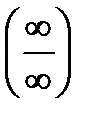, можно применить правило Лопиталя:
= 
= 
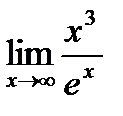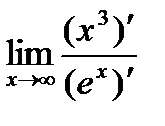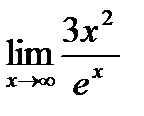. Снова получили неопределенность вида 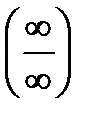, следовательно, можно применить правило Лопиталя еще раз:
= 
= 
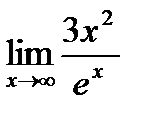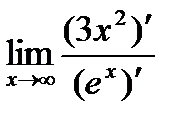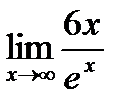. Повторно применяя правило Лопиталя, получим
= 
= 
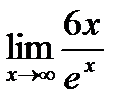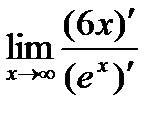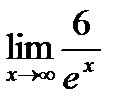=0, т.к. ех →∞ при х →∞.
Ответ: 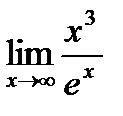=0.
Пример 3. Вычислите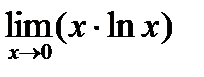 
.
Решение. Поскольку при х →0 функция lnx →∞, то имеет место неопределенность вида (0∙∞) и правило Лопиталя применить нельзя. Попытаемся преобразовать выражение, стоящее под знаком предела: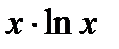 
= 
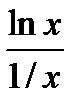. Тогда под знаком предела будет неопределенность вида 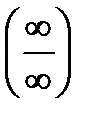, к которой правило Лопиталя применимо:
= 
= 
= 
= 
=- 
=- 
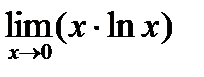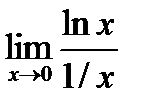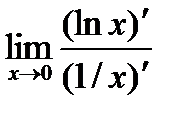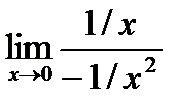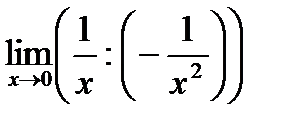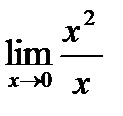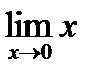=0.
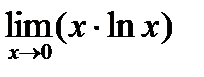Ответ: =0.
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 6, §6.3, стр. 127 – 130.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 37, стр. 218-220.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §5, стр. 239– 240.
