Критерий возрастания и убывания функции: пусть 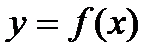 - дифференцируемая на интервале
- дифференцируемая на интервале 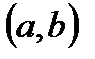 функция. Функция
функция. Функция 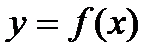 возрастает на
возрастает на 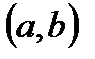 тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка.
тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка.
Функция 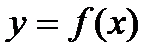 убывает на
убывает на 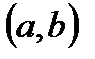 тогда и только тогда, когда её производная меньше или равна нулю в любой точке этого промежутка.
тогда и только тогда, когда её производная меньше или равна нулю в любой точке этого промежутка.
Критерий возрастания и убывания функции удобно представляется в виде схемы:
| f(x)ä | 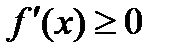 |
| f(x) æ | 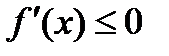 |
Критическими точками функции (первого рода) называются точки, в которых производная функции равна нулю или не существует.
Для нахождения промежутков монотонности функции используется следующий алгоритм:
1. Найдите область определения функции.
2. Найдите первую производную функции.
3. Определите критические точки первого рода (f'(xo) =0 или f'(xo) не существует).
4. На числовой оси отметьте критические точки и определите знаки производной на каждом из получившихся интервалов.
5. Выпишите интервалы монотонности.
Пример 1. Найдите промежутки монотонности функции 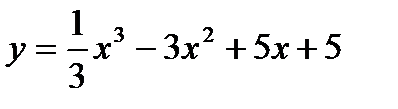 .
.
Решение. 1. Данная функция определена на множестве R.
2. Найдем первую производную функции: 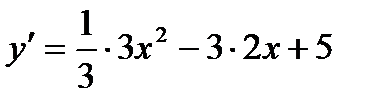 =
= 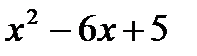 .
.
3. Определим критические точки первого рода (у' =0): 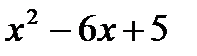 =0;
=0;
х 1=1 или х 2=5.
4. На числовой оси отметим критические точки х 1=1 и х 2=5. Эти точки разбивают область определения функции на три интервала (-∞;1), (1;5); (5;+∞). Расставим знаки производной функции у' = 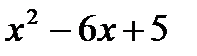 на каждом из полученных интервалов:
на каждом из полученных интервалов:
при х =0  (-∞;1) у' (0)=5>0;
(-∞;1) у' (0)=5>0;
при х =2  (1;5) у' (2)=
(1;5) у' (2)= 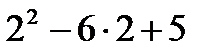 =-3<0;
=-3<0;
при х =6  (5;+∞) у' (6)=
(5;+∞) у' (6)= 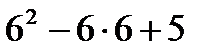 =5>0.
=5>0.
| х |
| + |
| + |
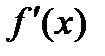 |
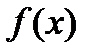 |
5. Согласно критерию возрастания и убывания функция 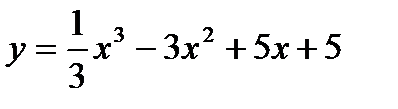 возрастает при х
возрастает при х  (-∞;1]
(-∞;1]  [5;+∞), убывает при х
[5;+∞), убывает при х  [1;5].
[1;5].
Ответ: 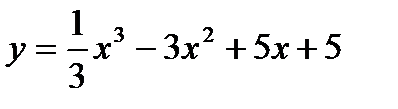 возрастает при х
возрастает при х  (-∞;1]
(-∞;1]  [5;+∞), убывает при х
[5;+∞), убывает при х  [1;5].
[1;5].
Пример 2. Найдите промежутки монотонности функции 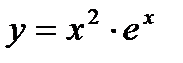 .
.
Решение. 1. Данная функция определена на множестве R.
2. Найдем первую производную функции по правилу производной произведения:
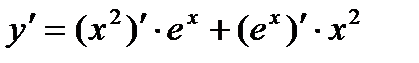 =
= 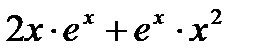 =
= 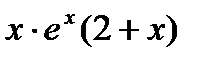
3. Определим критические точки первого рода (у' =0): 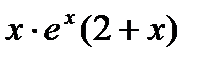 =0;
=0;
х 1=0 или 2+ х =0 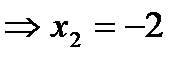
 (ех ≠0 для всех х из множества R).
(ех ≠0 для всех х из множества R).
4. На числовой оси отметим критические точки х =-2 и х =0. Эти точки разбивают область определения функции на три интервала (-∞;-2), (-2;0); (0;+∞). Расставим знаки производной функции у'= 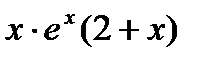 на каждом из полученных интервалов:
на каждом из полученных интервалов:
| -2 |
| х |
| + |
| + |
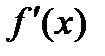 |
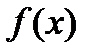 |
5. Согласно критерию возрастания и убывания функция 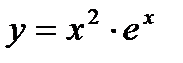 возрастает при
возрастает при
х  (-∞;-2]
(-∞;-2]  [0;+∞), убывает при х
[0;+∞), убывает при х  [-2;0].
[-2;0].
Ответ: 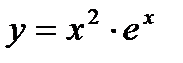 возрастает при х
возрастает при х  (-∞;-2]
(-∞;-2]  [0;+∞), убывает при х
[0;+∞), убывает при х  [-2;0].
[-2;0].
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 6, §6.3, стр. 126 – 127.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 38-39, стр. 220-226.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §7, стр. 255– 265.
 2015-04-01
2015-04-01 3016
3016
