Рассмотрим набор
| (x1, x2,..., xn), | (4.9) |
в котором переменные хi могут принимать значения 0 или 1. При этом число различных числовых наборов такого вида конечно и равно 2п (см. таблицу 4.2).
Определение 1. Функция, определенная на наборах вида (4.9) и принимающая в качестве своих значений на этих наборах 0 или 1, называется функцией алгебры логики (ФАЛ).
Так как число различных наборов значений аргументов является конечным, то любая функция алгебры логики может быть полностью задана конечной таблицей с 2 п строками (таблица 4.2). В левой части этой таблицы перечислены все наборы значений аргументов этой функции, а в правой части - значения функции на этих наборах.
Таблица 4.2 - Состояние (истинность)
логической функции f (х1, х2)
| х1 | х2 | f(х1, х2) |
Определение 2. Если две функции алгебры логики f1 (x1, x2,..., xn) и
f2 (x1, x2,..., xn) принимают на всех возможных наборах значений аргументов одинаковые значения, то функции fl и f2 называются равными (эквивалентными).
Факт равенства функций fl и f2 записывается обычным образом:
f1 (x1, x2,..., xn) = f2 (x1, x2,..., xn).
Определение 3. Функция f (x1,…, xi - 1, xi, xi + 1,..., xn) существенно зависит от аргумента xi, если имеет место соотношение
f (x1,…, xi - 1, 0, xi + 1,..., xn) ≠ f (x1,…, xi - 1, 1, xi + 1,..., xn).
В противном случае говорят, что от xi функция зависит несущественно и xi является ее фиктивным аргументом. Функция алгебры логики не изменится, если к ее аргументам дописать любое число фиктивных аргументов или зачеркнуть те аргументы, которые для данной функции являются фиктивными.
Пусть функция задана в виде таблицы 4.3.
Таблица 4.3 – Пример задания функции
| x1 | x2 | x3 | x4 | f (x1, x2, x3, x4) | x1 | x2 | x3 | x4 | f (x1, x2, x3, x4) |
Покажем, что аргумент x4 для этой функции является фиктивным. Для этого убедимся, что f (x1, x2, x3, 0 ) = f (x1, x2, x3, 1 ). Составим таблицу 4.4, определяющую функции f (x1, x2, x3, 0 ) и f (x1, x2, x3, 1 ).
Таблица 4.4 - Значение функций f (x1, x2, x3, 0 ) и f (x1, x2, x3, 1)
| x1 | x2 | x3 | f(x1, x2, x3, 0 ) | f(x1, x2, x3, 1 ) | x1 | x2 | x3 | f(x1, x2, x3, 0 ) | f(x1, x2, x3, 1 ) |
На основании определений 2 и 3 можно сделать вывод о фиктивности аргумента х4.
Теорема 1. Число различных функций алгебры логики, зависящих от п аргументов, конечно и равно 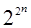 .
.
Для доказательства теоремы составим таблицу 4.5.
Таблица 4.5 – Функция алгебры логики
| x1 x2… xn-1 xn | f (x1, x2, …, x n) | x1 x2… xn-1 xn | f (x1, x2, …, xn) | |
| 0 0 … 0 0 | α1 | ………… | . | |
| 0 0 … 0 1 | α2 | ………… | . | |
| 0 0 … 1 0 | α3 | 1 1 … 1 1 | α2n | |
| ………… | . |
В этой таблице справа стоит одна из возможных функций алгебры логики (е1 ,…, еj,…, 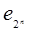 ), зависящая от n аргументов. Задавая тот или иной двоичный набор (е1 ,…, еj,…,
), зависящая от n аргументов. Задавая тот или иной двоичный набор (е1 ,…, еj,…, 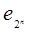 ), мы будем тем самым задавать одну из возможных функций алгебры логики. Но набор (е1 ,…, еj,…,
), мы будем тем самым задавать одну из возможных функций алгебры логики. Но набор (е1 ,…, еj,…, 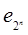 ) является набором вида (4.9) с 2n переменными. Различное число таких наборов равно
) является набором вида (4.9) с 2n переменными. Различное число таких наборов равно 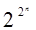 . Теорема доказана.
. Теорема доказана.
 2015-04-01
2015-04-01 953
953








