Методика определения сил в кинематических парах

Общие сведения. Силовой расчет механизмов заключается в определении сил в кинематических парах, а также неизвестных внешних сил или моментов. Результаты силового расчета необхо­димы для проведения прочностного расчета деталей механизма и определения механического КПД; в последнем случае силовой расчет проводится обязательно с учетом трения в кинематических парах.

Исходные данные для силового расчета: размеры, массы и моменты инерции звеньев, закон движения начального звена, одна из внешних сил (моментов), заданная графиком для всего цикла работы.

Силы взаимодействия звеньев будем обозначать буквой Q с двойным индексом. Первая цифра индекса показывает звено, со стороны которого действует сила; вторая цифра - звено, к кото­рому приложена сила, например, 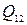- это сила, с которой звено 1 действует на звено 2.

Силовой расчет механизма будем производить методом с при­менением принципа Даламбера. При решении задачи к каждому зве­ну, помимо заданных внешних сил и моментов, силы тяжести, ис­комых сил в кинематических парах, прикладываются главный век­тор сил инерции 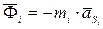и главный момент сил инерции 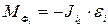. В результате вся система сил и моментов условно рассматривается в равновесии, и задачу динамики можно теперь решать методами статики.

Рассмотрение каждого, отдельно взятого звена с приложен­ными к нему силами и моментами не дает решения поставленной задачи, поскольку неизвестных больше, чем уравнений. Поэтому заданный плоский рычажный механизм расчленяется на первичный механизм и структурные, статически определимые группы Ассура, для которых число неизвестных равно числу уравнения.

Расчет начинают с той структурной группы, к звеньям ко­торой приложены известные внешние силы и моменты, а заканчивают первичным механизмом.

Определение сил в кинематических парах структурной груп­пы с вращательными парами (рис. 32). Заданы внешние силы моменты (например, 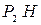, 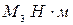), массы звеньев 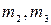в кг, моменты инерции звенье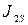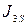в , в 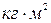относительно осей, проходящих через центры масс. Из плана ускорений определяем линейные ускорения 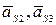в м/с² центров масс, угловые ускорения звеньев 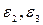, в рад/с и вычисляем главные векторы сил инерции звеньев 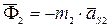, 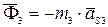в Н и глав­ные моменты сил 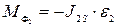, 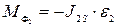в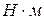

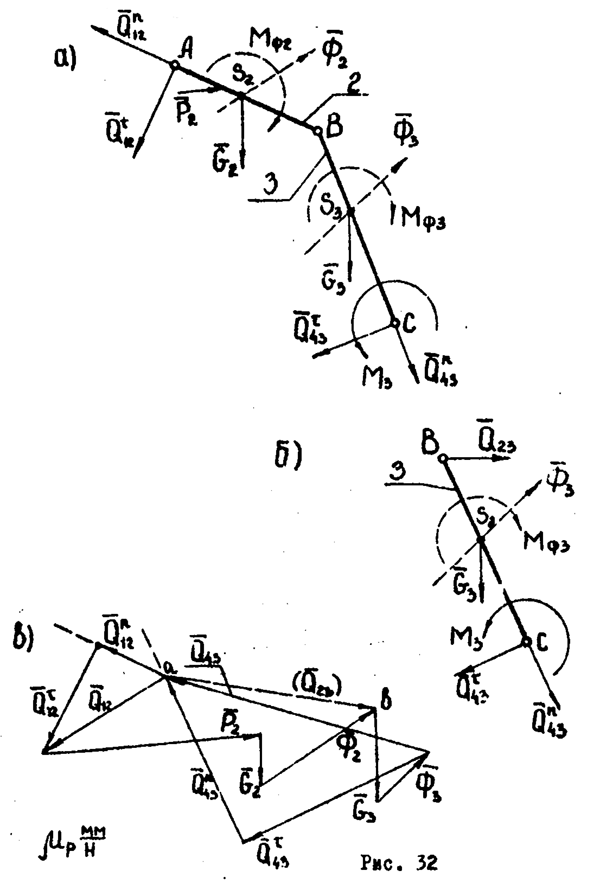
Силы во внешних шарнирах A и C разложим на составляющие, направленные по звену 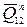, 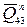и перпендикулярно к звену находим 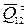, 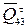(рис. 32а). Составляйте сил 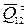и 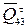находим из уравнений моментов сил относительно точки B для каждого звена в отдельности. Для звена 2

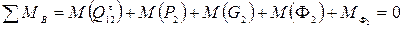(63)

где сила тяжести 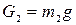Н; ускорение g =9,81 м/с².

Следует помнить, что в это уравнение числовые значения моментов подставляются со своими знаками.

Отсюда находим величину и направление 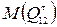, а затем

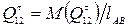
Аналогично для звена 3

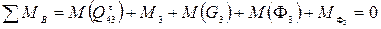(64)

откуда находим

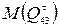и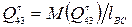

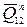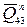Составляющие сил и определим из векторного уравнения сил для структурной группы, состоящей из звеньев 2 и 3:

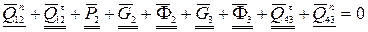(65)

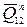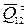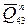В этом и последующих уравнениях одной чертой подчеркнуты век­торы, известные только по направлению, двумя чертами - из­вестные по величине и направлению. Составляющие сил (для наше­го примера и , и 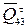) рекомендуется записывать рядом, чтобы впоследствии легко получить их векторную сумму ( 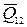и ).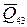

Уравнение (65) решим графически, строя план сил в некотором масштабе 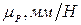(рис. 32в). Для этого сначала строим cyмму всех известных по величине и направлению векторов, а затем находим неизвестные по величине векторы сил 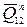и .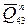

Для определения силы в шарнире B решим графически век­торное уравнение сил, приложенных к одному из звеньев, напри­мер, к звену 3 (рис. 32б)

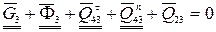(66)

Решение этого уравнения сводится к определению отрезка (ab), изображающего вектор 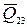(рис. 32в). Сила .

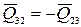Определение сил в кинематических парах структурной груп­пы с двумя вращательными и одной поступательной парами (рис.33).

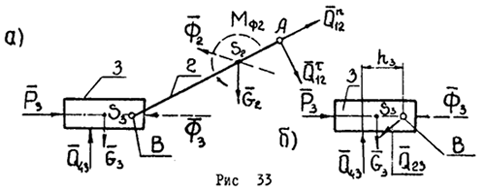
Заданы: внешняя сила 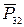в Н, массы звеньев 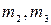в кг и момент инерции 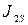в 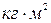. Вычислены главные векторы сил инер­ции 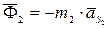, 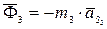и главный момент сил инерции 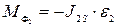в 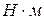; 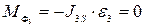, так как звено 3 движется поступательно. Для этой структурной группы, по сравнению с предыдущей, решение упрощается вследствие того, что сила 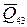известна по направлению. Силу в шарнире А раз­ложим на составляющие 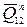и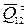

Из уравнения моментов сил, приложенных к звену 2, отно­сительно точки В

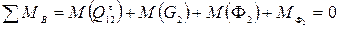(67)

находим 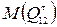и силу .

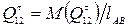Составляем векторное уравнение сил, приложенных к звень­ям 2, 3 структурной группы

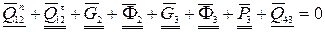(68)

Решая это уравнение графическим способом, находим неизвестные величины векторов 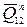и 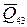. Плечо 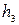найденной силы 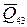(рис. 33б) получим из уравнения моментов сил, приложенных к звену 3, относительно точки B

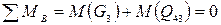(69)

Определим момент 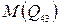, а зате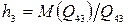м м.

Силу 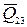находим из векторного уравнения сил, приложенных к звену 3,

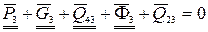(70)