2015-04-01
8209
Пусть некоторый опыт повторяется в неизменных условиях n раз, причём каждый раз может либо наступить (успех), либо не наступить (неудача) некоторое событие А, где Р (А) = р - вероятность успеха, Р (А) = 1- р = q - вероятность неудачи. Тогда вероятность того, что в k случаях из n произойдёт событие А вычисляется по формуле Бернулли
.
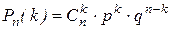Условия, приводящие к формуле Бернулли, называются схемой повторных независимых испытаний или схемой Бернулли. Так как вероятности Рn (k) для различных значений k представляют собой слагаемые в разложении бинома Ньютона
,
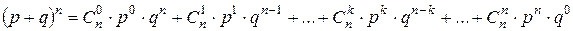то распределение вероятностей Рn (k), где 0£ k £ n, называется биномиальным.
При решении задач на использование формулы Бернулли часто применяют следующие формулы.
Вероятность наступления события А:
а) менее k раз
Pn (0)+ Pn (1)+…+ Pn (k- 1);
б) более k раз
Pn (k +1)+ Pn (k +2)+…+P n (n);
в) не менее k раз
P n (k)+ Pn (k +1)+…+ Pn (n);
г) не более k раз
Pn (0)+ Pn (1)+…+ Pn (k);
д) хотя бы один раз
1- Pn (0).
Пример 1. Что вероятнее: выиграть у равносильного противника (ничейный исход партии исключен) три партии из четырех или пять из восьми?
Решение. Так как противники равносильны, то вероятность успеха (выиграть партию) равна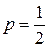 
, вероятность неудачи 
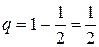. По формуле Бернулли находим
,
.
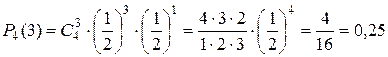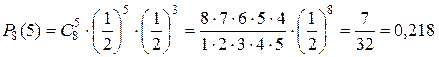Следовательно, выигрыш трех партий из четырех вероятнее, чем пять партий из восьми.
Пример 2. Всхожесть семян данного сорта оценена вероятностью р=0,8. Каковы вероятности того, что из 5 семян войдет: 0, 1, 2, 3, 4, 5.
Решение. Число опытов равно 5, опыты независимые. Вероятность появления события А (взошло семя) в каждом опыте одинакова и равна р=0,8, вероятность противоположного события q =0,2.
Следовательно, можно воспользоваться формулой Бернулли.
;
;
;
;
;
.
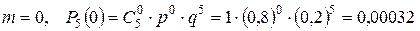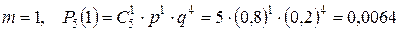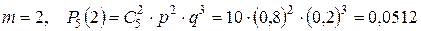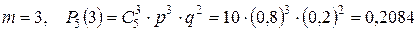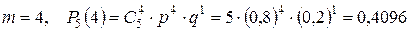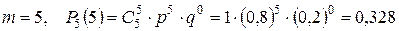Из примера2 следует, что вероятность Pn (k) для данного n с увеличением m от 0 до 5 сначала возрастает, а затем уменьшается. Число k 0, при котором Pn (k) имеет наибольшее значение, называется наивероятнейшим числом наступления успеха в n опытах. В приведенном примере k 0=4. Наивероятнейшее число можно найти из неравенства
.
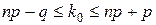Пример 3. Вероятность получения удачного результата при производстве сложного химического опыта равна 2/3. Найти наивероятнейшее число удачных опытов, если общее их число равно 7.
Решение. Вероятность успеха в одном опыте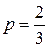 
, неудачи 
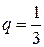, n = 7. Наивероятнейшее число удачных опытов k 0 найдем из неравенства
;
;
.
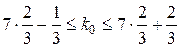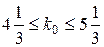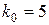Формулой Бернулли удобно пользоваться в том случае, когда число опытов n £10. При большом числе опытов по схеме Бернулли удобнее пользоваться приближенными формулами.
