Признак Даламбера

Ряд сходится, если .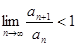

Если предел больше 1, то ряд расходится. Если предел равен 1, то ряд может быть как сходящимся, так и расходящимся. Признак Даламбера целесообразно применить, когда общий член ряда содержит выражение вида n! или .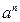

@ Задача 3. Исследовать на сходимость ряд .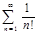

Решение: По признаку Даламбера 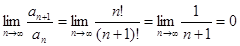, т.е. ряд сходится.

Признак Коши

Ряд сходится, если .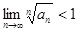

Если предел больше 1, то ряд расходится. Если предел равен 1, то ряд может быть как сходящимся, так и расходящимся. Признак Коши целесообразно применить, когда общий член ряда содержит выражение вида .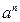

@ Задача 4. Исследовать на сходимость ряд .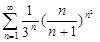

Решение: По признаку Коши 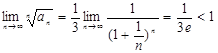, т.е. ряд сходится.