Интегральный признак Коши

Теорема: Если каждый член положительного ряда меньше предшествующего, то: а) если предел 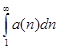конечный, то ряд (1) сходится, б) если предел бесконечный, то ряд (1) расходится.

@ Задача 5. Исследовать на сходимость гармонический ряд .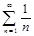

Решение: Из интегрального признака Коши 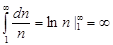следует, что ряд расходится.

Ряд называется знакопеременным, если его члены поочередно положительны и отрицательны. Достаточным признаком сходимости знакопеременного числового ряда являются признак Лейбница.