Дана линейно независимая система векторов
b 1, b 2,…, bl, al +1,…, a n l ≥ 1 (1)
часть, которой ортогональна, обозначим bl +1 ортогональную составляющую вектора аl +1 относительно ортогональной системы b 1, …, bl . .
Тогда
1. Система векторов
b 1, b 2, …, bl, bl +1, al +2, …, a n (2)
эквивалентна (1).
2. Система векторов (2) линейно независима, а ее часть b 1, b 2 …, bl +1 – ортогональна.
Используя, понятие ортогональной составляющей, опишем процесс превращения линейно независимой системы а 1, …, а n в ортогональную систему b 1, …, b n ненулевых векторов, который называется ортогонализацией системы а1, …, а n.
Этот процесс состоит из n –шагов, n –число векторов в исходной системе а 1, …, аn.
1 шаг. Полагаем b1=a1 и получаем систему
b 1, a 2, …, a n (3)
2 шаг. Заменим в системе (3) вектор а2 ортогональной составляющей относительно b1, и получим систему:
b 1, b 2, a 3,…, a n (4)
Согласно шагам ортогонализации система (4) линейно независима, а ее часть b 1, b 2–ортогональна.
Предположим, что уже построена линейно независимая система
b 1, b 2, …, b k-1, a k,…, a n, (5)
у которой b1, b 2, …, b k-1 – ортогональны.
На к-том шаге к = 3, n заменим в системе (5) вектор а к его ортогональной составляющей относительно системы b1, b 2, …, b k-1 и получим систему b 1, …, b k, a k+1, …, a n.
После выполнения n –го шага получим линейно независимую и ортогональную систему векторов b 1, …, b n.
Замечание. Если исходная система а 1, …, а n ортогональна, то ортогонализация не изменит ее.
Пример. Подвергнуть ортогонализации независимую систему векторов
а 1=(2, 0, 1, 1); а 2=(1, 2, 0, 1; а 3=(0, 1, -2, 0)
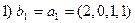
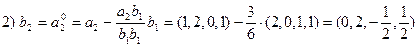
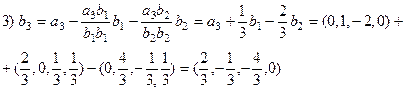
Теорема. Если вектор b разлагается по ортогональной системе a1, a2, …, an ненулевых векторов,
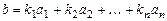 ,
,
то коэффициенты разложения могут быть рассчитаны так:
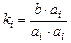 ,
, 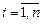 .
.
 2015-04-01
2015-04-01 6352
6352








