2015-04-01
5004
Для решения задач на собственные векторы и собственные значения в Mathcad встроено несколько функций, реализующих довольно сложные вычислительные алгоритмы:
- eigenvals(A) – вычисляет вектор, элементами которого являются собственные значения матрицы А;
- eigenvecs(A) – вычисляет матрицу, содержащую нормированные собственные векторы, соответствующие собственным значениям матрицы А.
Пример. Найти собственные значения и собственные векторы матрицы с помощью MathCad.
1. Задаем системную переменную и матрицы А (исходную) и Е (единичную):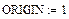 
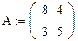
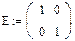
2. Находим собственные значения и собственные векторы матрицы А с помощью встроенных функций MathCad:
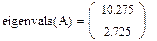
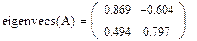
3. Находим собственные значения и собственные векторы матрицы А вручную. Для этого составляем характеристический определитель и вычисляем характеристический полином:
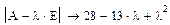
4. Приравниваем его нулю нажатием Ctrl+= (получаем характеристическое уравнение):
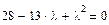
5. Находим корни характеристического уравнения с помощью символьных вычислений (подсвечиваем λ нажатием мыши и выбираем в меню Символы®Переменные®Вычислить, затем нажимаем символ =)
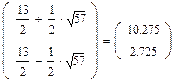
6. Присваиваем
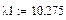
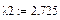
Это и есть собственные значения матрицы А.
7. Далее найдем собственные векторы матрицы А вручную. Для этого запишем левую часть системы уравнений:
,
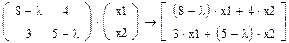где x1, x2 – элементы собственных векторов, соответствующих собственным значениям λ.
8. Получим собственный вектор, соответствующий собственному значению λ1:
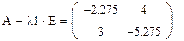
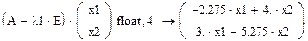
Запишем каждое уравнение системы отдельно (приравниваем их нулю нажатием Ctrl+=)
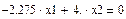
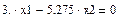
Из первого уравнения выразим х2 (подсвечиваем λ нажатием мыши и выбираем в меню Символы® Переменные® Вычислить)
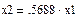
Принимаем х1=0.869 (согласно пункту 2)
Тогда х2=0.5688×0.869=0.494
Собственный вектор, соответствующий собственному значению λ1:
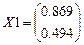
9. Получим собственный вектор, соответствующий собственному значению λ2:
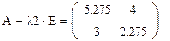
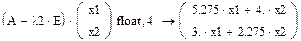
Запишем каждое уравнение системы отдельно (приравниваем их нулю нажатием Ctrl+=)
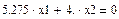
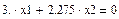
Из первого уравнения выразим х2 (подсвечиваем λ нажатием мыши и выбираем в меню Символы® Переменные® Вычислить)
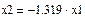
Принимаем х1=-0.604 (согласно пункту 2)
Тогда х2= –1.319×(–0.604)=0.797
Собственный вектор, соответствующий собственному значению λ2:
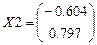
Для собственных векторов матрицы справедливы следующие утверждения:
1. Собственные векторы матрицы, отвечающие различным собственным значениям, линейно независимы.
2. Если число различных корней матрицы n -го порядка равно n, то в пространстве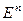 
существует базис из собственных векторов матрицы А (непосредственно следует из свойства 1).
3. Базис из собственных векторов матрицы А существует в том и только в том случае, когда сумма размерностей собственных подпространств равна n. Такая матрица называется матрицей простой структуры. Если 
– матрица простой структуры, то любой вектор из 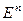является линейной комбинацией линейно независимой системы 
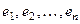собственных векторов этой матрицы.
4. Матрица простой структуры подобна диагональной матрице, т.е.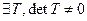 
, такая что
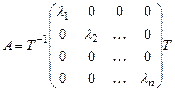, (8)
где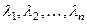 
– собственные значения матрицы .
5. Все корни характеристического многочлена симметрической матрицы действительны, т.е.
.
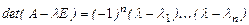6. Собственные векторы симметрической матрицы, отвечающие различным собственным значениям, ортогональны.
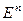7. Для симметрической матрицы в пространстве существует ортонормированный базис из собственных векторов.
Решим еще два примера на нахождение собственных векторов и собственных значений матрицы.
Пример 1. Найти собственные векторы и собственные значения матрицы
.
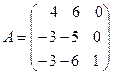Решение. Находим корни характеристического многочлена
= 
=
= 
:
, 
.
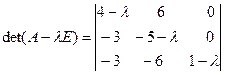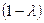
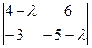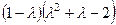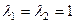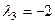Ищем собственные векторы с собственным значением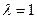 
, как решение системы 
:
.
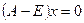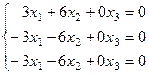
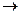
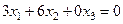Общее решение системы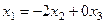 
. Фундаментальная система решений или базис пространства решений
, 
.
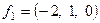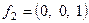Собственный вектор для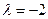 
находим из системы 
:
,
.
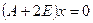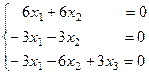
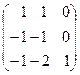
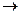
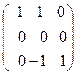
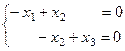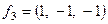Ответ. 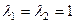, 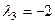– собственные значения,
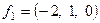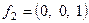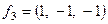, , – собственные векторы.
Пример 2. Найти ортонормированный базис из собственных векторов симметрической матрицы
.
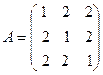Находим характеристический многочлен матрицы :
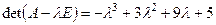. Целые корни ищем среди делителей свободного члена:
.
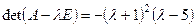Найдем собственные векторы с собственным значением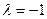 
.
.
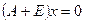
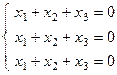
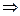
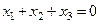
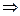
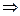
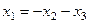Базис в пространстве решений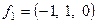 
, 
.
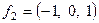Так как мы ищем ортонормированный базис, то ортогонализуем систему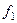 
, 
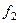. Получаем 
, 
, 
, 
, 
, 
.
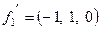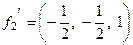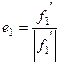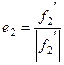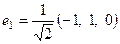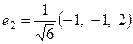Нашли ортонормированный базис в собственном подпространстве с собственным значением .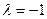
Найдем собственный вектор для собственного значения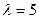 
:
.
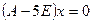
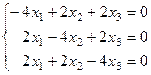Решаем методом Гаусса, получим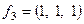 
, 
, 
.
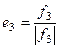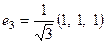Ответ. Искомый ортонормированный базис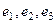 
.
Преобразование подобия (8) можно использовать для упрощения исходной матрицы, а задачу вычисления её собственных значений свести к аналогичной задаче для более простой матрицы. Очевидно, самым лучшим упрощением исходной матрицы было бы приведение её к треугольному виду:
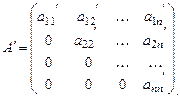
Тогда характеристическая матрица С так же имела бы треугольный вид. Как известно, определитель треугольной матрицы равен произведению ее диагональных элементов, поэтому характеристический многочлен в этом случае имеет вид:
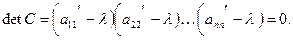(9)
Собственные значения матрицы, равные корням этого многочлена, можно получить сразу.
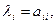
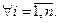(10)
Таким образом, собственные значения треугольной матрицы равны её диагональным элементам.
Некоторые типы матриц удается привести к треугольному виду с помощью преобразований подобия. В частности, симметрическую матрицу можно привести к диагональному виду. На практике часто используется приведение симметрической матрицы к трехдиагональному виду.
Существует ряд методов, основанных на преобразовании подобия, позволяющие привести исходную матрицу к более простой структуре.
