Теорема 4. Вектор  коллинеарен ненулевому вектору
коллинеарен ненулевому вектору  в том и только том случае, когда координаты вектора
в том и только том случае, когда координаты вектора  пропорциональны соответственным координатам вектора
пропорциональны соответственным координатам вектора  т.е.
т.е.
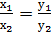 .
.
Линейные операции над векторами, заданными своими координатами в пространстве, производятся аналогично.
Пример 1. Пусть даны векторы  = {1;2;-1},
= {1;2;-1},  = {3;2;1},
= {3;2;1}, 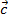 = {1;0;1} в некотором векторном базисе
= {1;0;1} в некотором векторном базисе  ,
,  ,
, 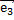 . Найти координаты линейной комбинации 2
. Найти координаты линейной комбинации 2  +3
+3  -4
-4 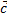 .
.
Решение. Введем обозначение для линейной комбинации 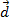 =2
=2 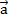 +3
+3 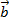 +(-4)
+(-4) 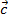 .
.
Коэффициенты линейной комбинации 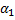 =2,
=2, 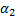 =3,
=3, 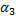 =-4. Запишем данное векторное равенство в координатной форме
=-4. Запишем данное векторное равенство в координатной форме 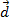 = {x,y,z}=
= {x,y,z}= 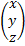 :
:
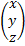 =2
=2 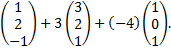
Очевидно, что каждая координата линейной комбинации векторов равна такой же линейной комбинации одноименных координат, т.е.
х = 2·1+3·3+(-4)·1=7,
у = 2·2+3·2+(-4)·0=10,
z = 2·(-1)+3·1+(-4)·0=-3.
Координаты вектора 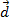 в базисе
в базисе  ,
,  ,
, 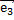 будут:
будут:
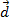 = {7,10,-3}
= {7,10,-3}
Ответ: 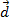 = {7,10,-3}.
= {7,10,-3}.
 2015-04-01
2015-04-01 934
934








