Декартовы (аффинные) координаты на плоскости

Выберем на плоскости О два неколлинеарных вектора и , образующих некоторый базис. Очевидно, что длины векторов и могут быть различны.

Определение 9. Совокупность {0; ; } точки О и векторного базиса , называют декартовой (аффинной) системой на плоскости.

Две прямые, проходящие через О и параллельные соответственно векторам , называют осями координат. Первую из них обычно называют осью абсцисс и обозначают Ох, вторую- осью ординат и обозначают Оу.

Будем всегда изображать и лежащими на соответствующих осях координат.

Определение 10. Координатами точки М на плоскости относительно декартовой (аффинной) системы координат {0; ; } называют координаты ее радиус-вектора 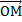по базису , :

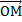= х +у , тогда числа х и у будет координатами М относительно декартовой(аффинной) системы координат {0; ; }. Координату х называют абсциссой точки М, координату у- ординатой точки М.

Итак, если выбрана система координат, {0; ; } на плоскости, то каждой точке М плоскости соответствует единственная точка М на плоскости: эта точка является концом вектора

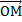= х +у .

Введение системы координат лежит в основе метода аналитической геометрии, сущность которой состоит в том, чтобы уметь сводить любую геометрическую задачу к задачам арифметики или алгебры.

Определение 11. Координатами вектора 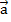на плоскости относительно декартовой системы координат {0; ; } называют координаты этого вектора в базисе , .

Чтобы найти координаты вектора 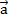, надо разложить его по базису , :

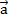= х +у , где коэффициенты х,у и будут координатами вектора 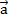относительно декартовой системы {0; ; }.