где
N – число молекул,
NA – постоянная Авогадро,
m – масса вещества,
M – молярная масса.
Уравнение Менделеева- Клайперона
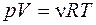 ,
,
где
р – давление газа,
V – его объем,
R – молярная газовая постоянная,
T – термодинамическая температура.
Уравнение молекулярно – кинетической теории газов
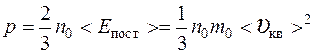 ,
,
где
n 0 – концентрация молекул,
< E пост> – средняя кинетическая энергия поступательного движения молекул,
m 0 – масса молекулы,
< υ кв> – средняя квадратичная скорость.
Средняя кинетическая энергия молекулы
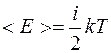 ,
,
где
k – постоянная Больцмана.
Внутренняя энергия идеального газа
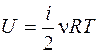 .
.
Скорости молекул:
средняя квадратичная 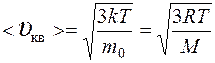 ,
,
наиболее вероятная 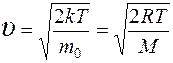 .
.
Средняя длина свободного пробега молекулы
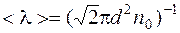 ,
,
где d – эффективный диаметр молекулы.
Среднее число столкновений молекулы в единицу времени
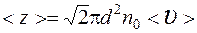 .
.
Уравнение диффузии
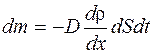 ,
,
где
D – коэффициент диффузии,
Ρ – плотность,
dS – элементарная площадка, перпендикулярная к оси Х.
Уравнение теплопроводности
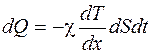 ,
,
где χ – коэффициент теплопроводности.
Сила внутреннего трения 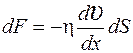 ,
,
гдеη – динамическая вязкость.
Вязкость (динамическая) 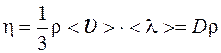 .
.
Теплопроводность 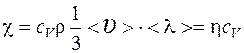 ,
,
где сV - удельная изохорная теплоемкость.
Молярная теплоемкость идеального газа:
Изохорная 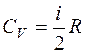 ,
,
Изобарная 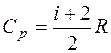 .
.
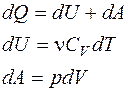
Работа расширения газа при процессе:
Изобарном 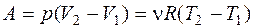 ,
,
Изотермическом 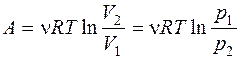 ,
,
адиабатном
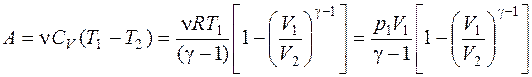 ,
,
где 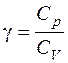 .
.
Уравнение Пуассона (уравнение адиабатного процесса)
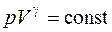 ,
, 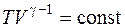 ,
, 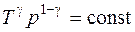 .
.
Коэффициент полезного действия цикла Карно
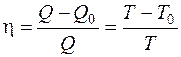 ,
,
где
Q и T – количество теплоты, полученное от нагревателя, и его температура,
Q 0 и T 0 – количество теплоты, переданное холодильнику, и его температура.
Изменение энтропии при переходе из состояния 1 в состояние 2
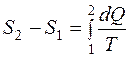
Уравнение Ван - дер - Ваальса:
для 1 моль газа 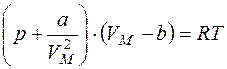 ,
,
для ν моль газа 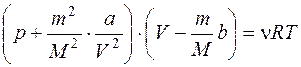 ,
,
где a и b – постоянные Ван - дер - Ваальса,
VM – объем 1 литра газа.
Собственный объем молекулы 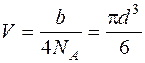 .
.
Высота поднятия жидкости в капилляре радиусом r
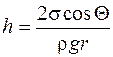 .
.
 2015-04-06
2015-04-06 1655
1655

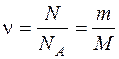 ,
,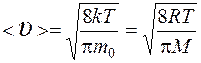 ,
,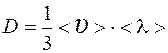 .
.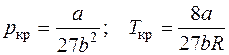 .
.






