В самом общем случае динамическое состояние классической системы определяется переменными положения, т.е. обобщенными координатами q1, q2, …, qR, и переменными скорости, т.е. производными по времени обобщенных координат 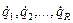 ; число степеней свободы системы обозначим буквой R. Если мы имеем дело с системой из n частиц, то в качестве переменных положения можно выбрать 3n декартовых координат этих частиц, но все последующее справедливо и при другом выборе координат. Положение системы в каждый момент времени может быть представлено в R-мерном конфигурационном пространстве точкой М, имеющей координаты q1, q2, …, qR. Задачей классической механики является нахождение законов эволюции системы во времени или законов движения точки М в конфигурационном пространстве.
; число степеней свободы системы обозначим буквой R. Если мы имеем дело с системой из n частиц, то в качестве переменных положения можно выбрать 3n декартовых координат этих частиц, но все последующее справедливо и при другом выборе координат. Положение системы в каждый момент времени может быть представлено в R-мерном конфигурационном пространстве точкой М, имеющей координаты q1, q2, …, qR. Задачей классической механики является нахождение законов эволюции системы во времени или законов движения точки М в конфигурационном пространстве.
Для очень большого числа динамических систем законы движения можно написать, вводя некоторую функцию, характеризующую систему, - функцию Лагранжа:
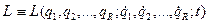 .
.
Координаты q удовлетворяют дифференциальным уравнениям второго порядка (уравнениям Лагранжа);
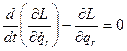 (r =1, 2, …, R).
(r =1, 2, …, R).
Величины
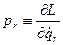
называются обобщенными импульсами Лагранжа. В том случае, когда qr есть одна из декартовых координат частицы с массой m, а силы получаются из статистического потенциала, величина pr есть соответствующая компонента количества движения этой частицы 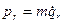 .
.
Законы движения могут быть также выражены в форме вариационного принципа. Действительно, система уравнений Лагранжа эквивалентна принципу наименьшего действия (Мопертюи – Гамильтон):
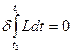 ,
, 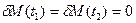 , (1)
, (1)
смысл которого состоит в следующем: из всех законов движения M(t), позволяющих системе перейти из положения M1 в момент времени t1 в положение М2 в момент времени t2, в действительности реализуется тот, который соответствует минимуму интеграла 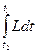 .
.
В обычном случае L представляет собой разность между кинетической энергией T (являющейся квадратичной функцией 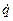 ) и потенциальной энергии V. Однако формализм Лагранжа применим при описании самого широкого класса динамических систем.
) и потенциальной энергии V. Однако формализм Лагранжа применим при описании самого широкого класса динамических систем.
В качестве примера рассмотрим электрон в кулоновском поле протона (предполагаемого бесконечно тяжелым). Пусть r (x,y,z) есть радиус-вектор электрона в системе координат с началом в точке, где находится протон, 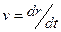 - скорость, p(px,py,pz) – импульс электрона. Функция Лагранжа есть
- скорость, p(px,py,pz) – импульс электрона. Функция Лагранжа есть
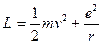 .
.
Обобщенный импульс электрона имеет координаты 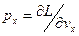 ,
, 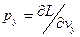 ,
, 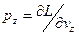 , которые равны составляющим его количества движения.
, которые равны составляющим его количества движения.
Аналогично можно получить уравнения движения, используя всякую систему координат. Для траекторий, расположенных в плоскости xy (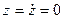 ), в полярных координатах получаем (
), в полярных координатах получаем (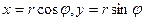 )
)
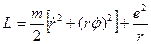 ,
, 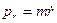 ,
, 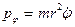 ,
,
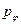 равно абсолютной величине момента количества движения; это действительно интеграл движения.
равно абсолютной величине момента количества движения; это действительно интеграл движения.
2.15. Квантование свободного электромагнитного поля.
Рассматривая электромагнитное поле как квантовый объект, удобно исходить из такого классического описания поля, в котором оно характеризуется хотя и бесконечным, но дискретным рядом переменных; такое описание позволит непосредственно применить обычный аппарат квантовой механики. Представление же поля с помощью потенциалов, задаваемых в каждой точке пространства, есть по существу описание с помощью непрерывного множества переменных.
Пусть A ( r, t) – векторный потенциал свободного электромагнитного поля, удовлетворяющий «условию поперечности»
div A =0. (1)
При этом скалярный потенциал Ф=0, а поля Е и Н:
Е = - А, Н = rot A. (2)
Уравнения Максвелла сводятся к волновому уравнению для А:
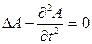 . (3)
. (3)
Поле в конечном объеме может быть разложено на бегущие плоские волны, так что его потенциал изобразится рядом вида:
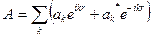 , (4)
, (4)
где коэффициенты 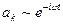 ,
, 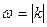 . (5)
. (5)
В силу условия (1) комплексные векторы ak ортогональны соответствующим волновым векторам: a kk=0.
Заданием векторов a k полностью определяется поле в данном объеме.
Канонические переменные поля определяются посредством
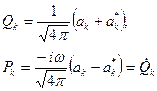 (6)
(6)
Векторный потенциал выражается через канонические переменные согласно
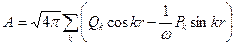 . (7)
. (7)
Для нахождения функции Гамильтона надо вычислить полную энергию поля 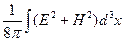 , выразив ее через величины Qk, Pk. Представив А в виде разложения (7), вычислив Е и Н согласно (2) и произведя интегрирование, получим
, выразив ее через величины Qk, Pk. Представив А в виде разложения (7), вычислив Е и Н согласно (2) и произведя интегрирование, получим
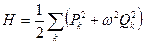 .
.
Обозначив две компоненты векторов Qk, Pk (в плоскости, перпендикулярной k) посредством 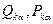 (
(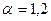 ), перепишем ф-цию Гамильтона в виде:
), перепишем ф-цию Гамильтона в виде:
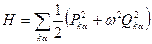 . (8)
. (8)
Таким образом, ф-ция Гамильтона распадается на сумму независимых членов, каждый из которых содержит только по одной паре величин 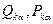 .
.
Перейдем теперь к квантованию свободного электромагнитного поля. Изложенный способ классического описания поля делает очевидным путь перехода к квантовой теории. Мы должны рассматривать теперь канонические переменные – обобщенные координаты 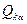 и обобщенные импульсы
и обобщенные импульсы 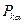 - как операторы с правилом коммутации:
- как операторы с правилом коммутации:
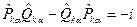 (9)
(9)
В результате для гамильтониана получается выражение:
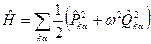 , (10)
, (10)
в точности соответствующее классической функции Гамильтона.
Для уровней энергии поля: 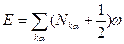 , (11) где
, (11) где 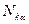 - целые числа.
- целые числа.
 2015-04-08
2015-04-08 1065
1065
