| Наименование средней | Формула средней | |
| простая | взвешенная | |
| Арифметическая | 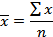
| 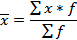
|
| Гармоническая | 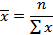
| 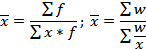
|
| Геометрическая |  ; ;
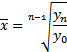
| 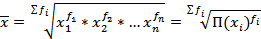
|
| Квадратическая | 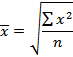
| 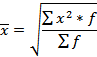
|
Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получившие широкое применения в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.
Средняя квадратическая применяется для расчета среднего квадратического отклонения (σ), являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).
Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики, если промежутки времени, к которым относятся коэффициенты роста, одинаковы. Если средние коэффициенты роста относятся к периодам различной продолжительности, то общий средний коэффициент роста за весь период определяется по формуле средней геометрической взвешенной.
Среди структурных средних, характеризующих структуру совокупности, наиболее известны мода и медиана.
Мода и медиана в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.
Медиана (Ме) – значение изучаемого признака, которое по своей величине занимает серединное место в ряду вариантов, расположенных в порядке их возрастания или убывания. Такой ряд называется ранжированным. Примером такого ряда может служить месячная заработная плата рабочих цеха.
| Порядковый номер рабочего | Итого | |||||||
| Месячная заработная плата, руб |
В этом ряду среднее место по размеру заработной платы занимает рабочий с номером 4, получивший 160 руб. эта величина и есть медиана. Меньше и больше медианы одинаковое число вариантов. Порядковый номер, которому соответствует медиана, определяется по формуле:
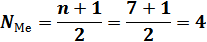
Если количество вариантов в ряду четное число, т.е., если бы в цехе был еще и восьмой рабочий с заработной платой 276 руб., то медиана находилась бы посередине между четвертым и пятым порядковыми номерами.
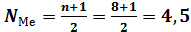 В таких случаях принято считать, что в промежутке между номерами идет равномерное нарастание или убывание вариантов. Поэтому за медиану принимают среднюю арифметическую из вариантов с номерами четыре и пять. В данном примере Ме = (х4 +х5) / 2 = (160+175) / 2 = 167,5 руб.
В таких случаях принято считать, что в промежутке между номерами идет равномерное нарастание или убывание вариантов. Поэтому за медиану принимают среднюю арифметическую из вариантов с номерами четыре и пять. В данном примере Ме = (х4 +х5) / 2 = (160+175) / 2 = 167,5 руб.
Смысл полученного результата такой: одна половина рабочих получила за месяц меньше, а другая – больше 167,5 руб. Медиана, следовательно, обобщающий показатель распределения совокупности, уровень признака, который делит совокупность на две равные части.
Приведенный пример вычисления медианы относится к случаю, когда расчет производится на основе индивидуальных значений признака. Обычно же в статистике приходится иметь дело со сгруппированными данными в форме дискретных и интервальных рядов. В таком случае медиана вычисляется по следующей формуле:
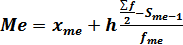
где хе – нижняя граница медианного интервала; h – величина медианного интервала; ∑f –сумма частот или частостей ряда; S mе – 1 - сумма накопленных частот в интервалах, предшествующих медианному; fmе – частота медианного интервала.
Мода (Мо) – это вариант признака, который при данном сочетании причин разного порядка чаще всего встречается в вариационном ряду. Например, цена, по которой чаще всего реализуется данный товар на рынке, является модой или модальной ценой. Месячная заработная плата, которая чаще встречается в данном коллективе, является для него модальной заработной платой. Мода отвечает на вопрос о том, какое значение изучаемой переменной величины наиболее вероятно. То, что в статистике принято называть модой, считается в обычной жизни массовым, типичным, типическим.
В дискретных рядах мода легко определяется как вариант, которому соответствует максимальная частота. Определение моды в интервальных рядах требует расчета по формуле:
fmo – fmo-1
Mo = xmo + h ----------------------------------,
(fmo – fmo-1) + (fmo – fmo+1) 
где хmo — нижняя граница модального интервала; h — величина модального интервала; fmo — частота модального интервала; fmo+1 — частота интервала, следующего за модальным; fmo-1 — частота интервала, предшествующего модальному.
В средней находит отражение то общее, что свойственно всем единицам совокупности. Но каждой единице свойственны и индивидуальные особенности, которые ведут к отклонениям от среднего уровня. Таковы, например, отклонения выработки отдельных рабочих от средней выработки по цеху, которые имеют место даже, если все рабочие производят одни и те же изделия из одного и того же сырья и на одних и тех же станках. Эти отклонения вызваны индивидуальными особенностями рабочих - опытом и знанием дела, состоянием здоровья и самочувствием, сообразительностью и инициативностью и т. п. Поэтому изучение отклонений от средней, их причины, масштабы, а также закономерности их распределения представляет большой практический и теоретический интерес. Эти задачи решаются в определенной мере при помощи показателей вариации.
К абсолютным показателям вариации относятся:
· размах вариации (колебаний);
· среднее линейное отклонение;
· среднее квадратическое отклонения;
· дисперсия.
Размахом вариации называют амплитуду колебаний, определяемую как разность между максимальным и минимальным значениями признака, положенного в основу ряда распределения. Если обозначить максимальное значение хmax, а минимальное — хmin, то размах вариации R равен:
R = xmax — xmin, где х — вариант признака. Этот показатель представляет интерес в тех случаях, когда важно знать, какова амплитуда колебания признака и в каких пределах он колеблется.
Среднее линейное отклонение (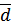 ) и среднее квадратическое отклонение (σ) показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.
) и среднее квадратическое отклонение (σ) показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.
Среднее линейное отклонение определяется по формулам:
а) для несгруппированных данных
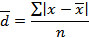
б) для вариационного ряда
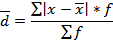
Среднее квадратическое отклонение (σ) и дисперсия (σ2) определяются так:
а) для несгруппированных данных
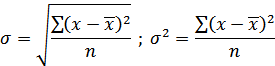
б) для вариационного ряда
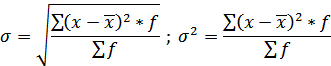
Формула для расчета дисперсии может быть преобразована:
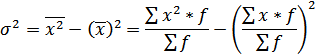
т.е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины.
При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации.
Наиболее часто применяется коэффициент вариации. Его применяют не только для сравнительной оценки вариации, но и для характеристики однородной совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному):
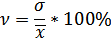
Кроме общей средней для всей совокупности исчисляются средние по отдельным группам (групповые или частные средние) и три показателя дисперсии:
· общая дисперсия;
· межгрупповая дисперсия;
· средняя внутригрупповая дисперсия.
Величина общей дисперсии (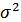 ) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности, и определяется по формуле:
) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности, и определяется по формуле:
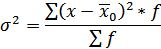
где 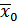 - общая средняя арифметическая для всей изучаемой совокупности.
- общая средняя арифметическая для всей изучаемой совокупности.
Межгрупповая дисперсия (дисперсия групповых средних 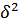 ) отражает систематическую вариацию, т.е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки. Межгрупповая дисперсия определяется по формуле:
) отражает систематическую вариацию, т.е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки. Межгрупповая дисперсия определяется по формуле:
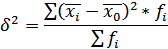
где 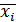 -средняя по отдельной группе;
-средняя по отдельной группе;
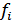 - число единиц в определенной группе.
- число единиц в определенной группе.
Средняя внутригрупповая дисперсия (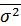 ) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.
) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.
Средняя внутригрупповая дисперсия определяется по формуле:
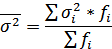
где 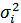 - дисперсия по отдельной группе:
- дисперсия по отдельной группе:
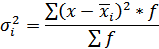
Указанные дисперсии взаимосвязаны между собой следующим равенством: величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии:
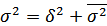
Это тождество отражает закон (правило) сложения дисперсий. Опираясь на это правило, можно определить, какая часть (доля) общей дисперсии складывается под влиянием признака-фактора, положенного в основу группировки.
Существует также вариация альтернативного признака. Альтернативный признак – качественный признак, имеющий две взаимоисключающие разновидности (например, работники предприятия подразделяются на мужчин и женщин; продукция-на годную и бракованную и т.д.).
Альтернативный признак принимает всего два значения:
1-наличие признака;
0-отсутствие признака.
p+q=1,
где р – доли единиц, обладающих признаком;
q –доли единиц, не обладающих признаком.
Среднее значение альтернативного признака
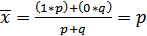
Дисперсия альтернативного признака
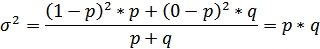
Предельное значение вариации альтернативного признака равно 0,25; оно получается при p=q=0,5.
 2015-04-30
2015-04-30 2828
2828
