Производственная функция

Производственной функцией называется зависимость производственного результата от используемых в данном процессе ресурсов. Производственные функции предназначены для моделирования процесса производства некоторой хозяйственной единицы: отдельной фирмы, отрасли или всей экономики государства в целом.

С их помощью решаются задачи:

— оценки отдачи ресурсов в производственном процессе;

— прогнозирования экономического роста;

— разработки вариантов плана развития производства;

— Оптимизации функционирования хозяйственной единицы при условии заданного критерия и ограничений по ресурсам.

Общий вид производственной функции: 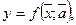где 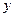— ожидаемый результат; 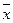— вектор ресурсов; 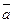— вектор параметров, рассчитываемый на основе статистики.

Предполагается, что производственная функция должна быть

непрерывной и дважды дифференцируемой.

Экономические предположения состоят в следующем:

При отсутствии хотя бы одного производственного ресурса

производство невозможно; рост использования ресурсов приводит к росту результата

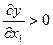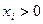
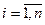производства, т.е. выполняется соотношения: при ; увеличение затрат одного ресурса приводит к снижению эффективности его использования:

.

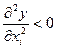
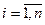Чаще всего производственные функции строятся на базе степенной

зависимости 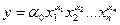. Если 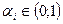, эти функции обладают свойствами, которые достаточно соответствуют закономерностям поведения реальных экономических субъектов.

Типичным примером производственной функции степенного вида

является функция Кобба-Дугласа. В 1928 г. Ч. Кобб и П. Дуглас на основе данных по обрабатывающей промышленности США за период 1899-1922 гг. предоставили функцию

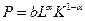, где 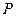— расчетный индекс производства; 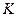— индекс основного капитала; 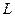— индекс занятости.

Производственная функция Кобба-Дугласа устанавливает зависимость

величины созданного общественного продукта от совокупных затрат живого труда 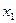и суммарного объема применяемых производственных фондов 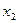.Она имеет следующий вид:

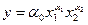, (1)

где 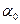— коэффициент, учитывающий влияние факторов, не вошедших в это уравнение, их конкретные числовые значения определяются на основе статических данных с помощью корреляционных методов, соблюдаются условия 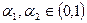.Обозначим 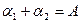. Эта сумма показывает эффект одновременного пропорционального увеличения объема как ресурсов труда, так и производственных фондов. Если 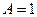, то увеличение ресурсов в 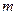раз приводит к увеличению объема производства также в 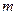раз. Если 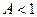, то увеличение ресурсов опережает увеличение выпуска. Если 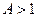, то увеличение выпуска опережает увеличение роста ресурсов. Можно говорить о положительном эффекте расширения производства.

Каждый из ресурсов характеризуется средней и предельной величиной.

Разделив обе части уравнения (1) на 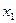, мы получаем среднюю производительность труда:

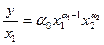(2)

Средняя производительность труда показывает, сколько единиц выпускаемой продукции приходится на единицу затрачиваемого труда. Поскольку коэффициент 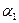меньше 1, показатель степени 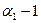является отрицательной величиной, следовательно, с увеличением затрат труда средняя производительность труда снижается. Однако, в реальном производстве дополнительно привлекаемая рабочая сила обеспечивается и дополнительными средствами производства, т.е. производительность труда снижается с ростом трудовых затрат при прочих равных условиях.

В анализе производственных функций наряду со средними показателями существенную роль играют предельные величины. Предельная производительность труда показывает, сколько дополнительных единиц продукции приносит дополнительная единица затраченного труда.

.

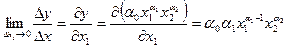Вторая частная производная 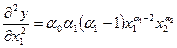(3)

Так как 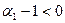, а все остальные множители в правой части (3)

положительны, то 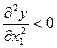.Вторая частная производная отрицательна, следовательно, предельная производительность с ростом 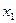уменьшается.

Сравнивая формулы (2) и (3), получаем 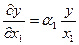. (4)

Поскольку 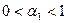, можно сделать вывод, что для производственной

функции Кобба-Дугласа предельная производительность труда всегда ниже средней производительности.

Наряду с вычислением абсолютного прироста продукции на единицу

прироста затрат можно определить показатель, характеризующий относительный прирост объема производства на единицу относительного увеличения ресурсов труда. Пользуясь выражением (4), получаем

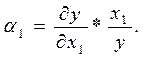
Полученный показатель называется эластичностью выпуска продукции

по затратам труда. Эластичность выпуска показывает, на сколько процентов

увеличивается выпуск при увеличении затрат труда на 1%. Предельная производительность от объемов ресурсов не зависит, и при любом их сочетании увеличение трудовых затрат на 1% приводит к росту объема производства на %.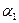

Аналогичные показатели можно рассчитать по отношению ко второму

фактору функции (1) – производственным фондам. Объем продукции в расчете на единицу используемых производственных фондов называется фондоотдачей. Можно рассчитать среднюю и предельную фондоотдачу. Из формулы (1) получаем

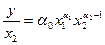
Показатель предельной фондоотдачи определяется как частная

производная выпуска продукции по объему фондов:

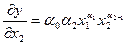
Предельная фондоотдача отличается от средней лишь сомножителем

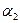. Поскольку положительный коэффициент 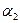меньше единицы, предельная фондоотдача в производственной функции (1) всегда ниже средней.

Относительная предельная фондоотдача, или эластичность выпуска

продукции по объему производственных фондов, определяется выражением:

.

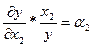Как и по отношению к затратам труда, эластичность выпуска по фондам есть величина постоянная, равная коэффициенту регрессии .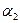

Производственная функция позволяет рассчитать потребность в одном

из ресурсов при заданном объеме производства и величине другого ресурса. Из уравнения (1) следует, что потребность в ресурсах труда равна: 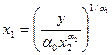(5).

Если заданы ресурсы труда и объем продукции, то потребность в

производственных фондах составляет .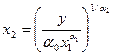

Производственная функция позволяет исследовать и вопросы соотношения, замещения, взаимодействия ресурсов. В частности, в экономике при изучении взаимодействия трудовых ресурсов и производственных фондов определяется важный показатель – фондовооруженность труда. Для функции вида (1) фондовооруженность труда 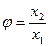(отношение переменных 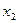и ).

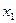Взаимодействующие в рамках производственной функции ресурсы

могут в известном смысле замещать друг друга. Это означает, что единицу одного ресурса можно заменить некоторым количеством другого ресурса так, что объем продукции при этом останется прежним.

На основе производственной функции можно рассчитать предельную норму замещения ресурсов, используя частные производные ;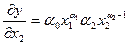

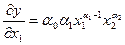. Так, предельная норма замещения затрат труда производственными фондами для функции вида (1) равна: 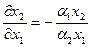. Знак минус показывает, что с увеличением одного ресурса объем второго ресурса должен быть снижен.