Определение

Определенный интеграл

Понятие определённого интеграла Римана.

Пусть – произвольная, ограниченная на отрезке функция. Рассмотрим разбиение T отрезка на конечное число частей:

.

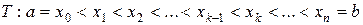В каждом частичном отрезке 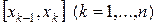выберем произвольную точку 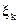и составим сумму, зависящую от разбиения T и выбора точек 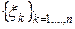. Сумма произведений значения функции в точке 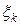на длину соответствующего частичного отрезка разбиения 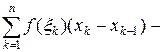это интегральная сумма Римана для функции , составленная по данному разбиению T.

Обозначим через 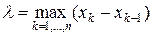мелкость разбиения T.

Определение.

Если существует конечный предел интегральных сумм при 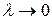, и этот предел на зависит ни от выбора разбиения, ни от выбора точек 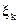внутри каждого частичного отрезка разбиения, то такой предел называется определённым интегралом Римана от функции на отрезке

.

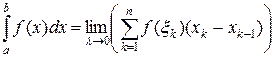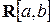– класс функций, интегрируемых по Риману на отрезке .