1) Для одной и той же функции и конкретного разбиения верхняя сумма Дарбу всегда не меньше, чем нижняя: 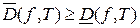 .
.
2) При измельчении разбиения, то есть при добавлении новых точек к исходному разбиению, верхние суммы Дарбу для одной и той функции
не увеличиваются, а нижние суммы Дарбу не уменьшаются.
3) Для одной и той же функции и любых разбиений 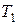 и
и 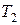 верхняя сумма Дарбу, соответствующая разбиению
верхняя сумма Дарбу, соответствующая разбиению 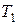 , не меньше, чем нижняя сумма Дарбу, соответствующая разбиению
, не меньше, чем нижняя сумма Дарбу, соответствующая разбиению 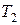 :
:
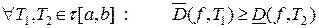 .
.
Доказательства этих свойств можно найти в литературе.
Зафиксируем некоторое разбиение 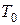 . Рассмотрим семейство всех верхних сумм Дарбу
. Рассмотрим семейство всех верхних сумм Дарбу 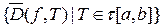 . В силу свойства 3) сумм Дарбу,
. В силу свойства 3) сумм Дарбу,
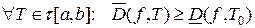 , то есть множество всех верхних сумм Дарбу ограничено снизу, поэтому существует конечная точная нижняя грань у этого множества и эта величина называется верхним интегралом Римана от функции
, то есть множество всех верхних сумм Дарбу ограничено снизу, поэтому существует конечная точная нижняя грань у этого множества и эта величина называется верхним интегралом Римана от функции  по отрезку
по отрезку  :
: 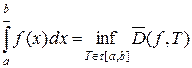 .
.
Аналогично существует конечная точная верхняя грань у множества всех нижних сумм Дарбу и эта величина называется нижним интегралом Римана от функции  по отрезку
по отрезку  :
: 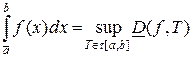 .
.
Определение. Если верхний интеграл равен нижнему, то функция  является интегрируемой по Риману на отрезке
является интегрируемой по Риману на отрезке  и интеграл Римана равен любому из этих значений. То есть из равенства
и интеграл Римана равен любому из этих значений. То есть из равенства
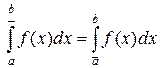 следует, что
следует, что 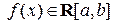 и выполняется равенство
и выполняется равенство
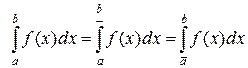 .
.
 2015-05-05
2015-05-05 910
910








