Рассмотрим сначала однородный стержень длины L, имеющий постоянную линейную плотность P. Тогда масса стержня находится по формуле
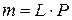 .
.
Пусть теперь стержень неоднородный, имеющий длину L и переменную линейную плотность. Выведем формулу для массы такого стержня. Расположим стержень на оси  . Начало стержня обозначим точкой
. Начало стержня обозначим точкой 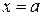 , конец стержня в точке
, конец стержня в точке 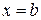 . Плотность стержня в точке
. Плотность стержня в точке 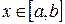 обозначим
обозначим 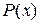 . Рассмотрим случай, когда функция
. Рассмотрим случай, когда функция 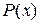 непрерывна на отрезке
непрерывна на отрезке  . Разобьем отрезок
. Разобьем отрезок  на конечное число частей точками
на конечное число частей точками 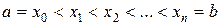 . Обозначим через
. Обозначим через 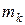 массу стержня, соответствующую частичному отрезку разбиения
массу стержня, соответствующую частичному отрезку разбиения
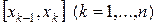 . Тогда масса стрежня равна сумме масс всех таких его частей
. Тогда масса стрежня равна сумме масс всех таких его частей 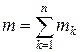 . Если части достаточно маленькие, то функция
. Если части достаточно маленькие, то функция 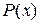 в силу непрерывности не может сильно измениться на отрезке
в силу непрерывности не может сильно измениться на отрезке 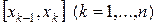 , поэтому на каждом таком отрезке функцию
, поэтому на каждом таком отрезке функцию 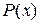 можно считать постоянной, и равной значению в любой точке отрезка. Выберем внутри каждого отрезка точку
можно считать постоянной, и равной значению в любой точке отрезка. Выберем внутри каждого отрезка точку 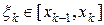 . Будем считать плотность стержня на отрезке
. Будем считать плотность стержня на отрезке 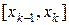 постоянной и равной
постоянной и равной 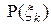 . Тогда верно приближенное равенство
. Тогда верно приближенное равенство
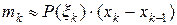 . Масса всего стержня тогда приблизительно равна
. Масса всего стержня тогда приблизительно равна
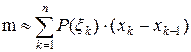 .
.
Если длину наибольшего из частичных отрезков разбиения 
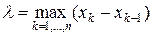 устремить к нулю, то приближенное равенство для массы становится точным и верна формула
устремить к нулю, то приближенное равенство для массы становится точным и верна формула
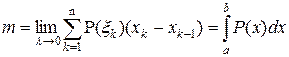 .
.
 2015-05-05
2015-05-05 3770
3770
