Пусть задана 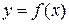 – непрерывная функция на отрезке
– непрерывная функция на отрезке  , эта функция неотрицательна, то есть
, эта функция неотрицательна, то есть 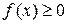
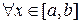 .
.
Криволинейная трапеция – это
фигура, которая ограничена снизу осью 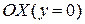 , сверху графиком
, сверху графиком
непрерывной неотрицательной
функции 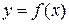 , по бокам вертикальными прямыми
, по бокам вертикальными прямыми 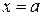 ,
, 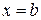 .
.
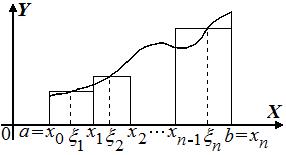
Рассмотрим произвольное разбиение T
отрезка  точками
точками
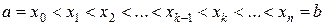 .
.
Выберем точки 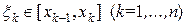 внутри каждого частичного отрезка разбиения. Произведение значения функции в точке
внутри каждого частичного отрезка разбиения. Произведение значения функции в точке 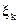 на длину частичного отрезка
на длину частичного отрезка 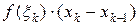 геометрически является площадью прямоугольника с основанием
геометрически является площадью прямоугольника с основанием 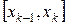 и длиной высоты
и длиной высоты 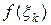 . Тогда интегральная сумма Римана
. Тогда интегральная сумма Римана 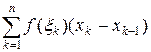 представляет собой площадь ступенчатой фигуры, составленной из таких прямоугольников. При измельчении разбиения, то есть при
представляет собой площадь ступенчатой фигуры, составленной из таких прямоугольников. При измельчении разбиения, то есть при 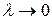 , площадь ступенчатой фигуры стремится к площади криволинейной трапеции:
, площадь ступенчатой фигуры стремится к площади криволинейной трапеции:
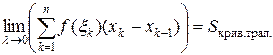 .
.
Геометрический смысл определённого интеграла.
Определенный интеграл от неотрицательной непрерывной функции 
на отрезке  равен площади криволинейной трапеции, лежащей под графиком этой функции
равен площади криволинейной трапеции, лежащей под графиком этой функции 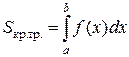 .
.
Иногда можно вычислить определенный интеграл, пользуясь только его геометрическим смыслом.
Пример 1. Вычислить интеграл 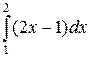 .
.
Подынтегральная функция 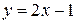 непрерывна и положительна на отрезке
непрерывна и положительна на отрезке
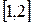 . Тогдавеличина интеграла равна площади фигуры под графиком этой функции. Эта фигура является обычной трапецией, по формуле площади трапеции находим
. Тогдавеличина интеграла равна площади фигуры под графиком этой функции. Эта фигура является обычной трапецией, по формуле площади трапеции находим
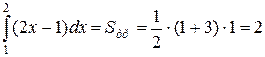 .
.
Пример 2. Вычислить интеграл 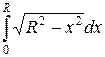 .
.
Подынтегральная функция 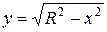 непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке 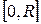 . Тогдавеличина интеграла равна площади фигуры под графиком этой функции. Эта фигура является четвертью круга радиуса
. Тогдавеличина интеграла равна площади фигуры под графиком этой функции. Эта фигура является четвертью круга радиуса 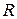 .
.
По формуле площади круга, находим значение интеграла
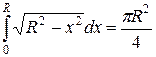 .
.
 2015-05-05
2015-05-05 3845
3845
