Рассмотрим общий случай, когда кривая задана параметрическими уравнениями
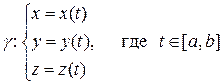 .
.
Обозначим через 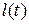 переменную длину дуги на отрезке
переменную длину дуги на отрезке 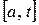 .
.
Известна формула для дифференциала длины дуги
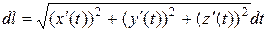 . Отсюда длина дуги, соответствующая изменению параметра
. Отсюда длина дуги, соответствующая изменению параметра 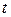 на отрезке
на отрезке  , вычисляется по формуле
, вычисляется по формуле
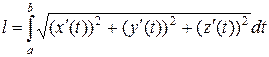 (8.1)
(8.1)
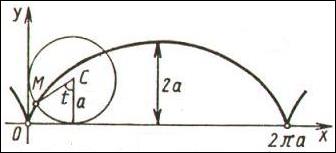 Пример. Найти длину одной арки циклоиды.
Пример. Найти длину одной арки циклоиды.
Циклоида – это траектория фиксированной точки, находящейся на ободе колеса, катящегося без проскальзывания. Параметрические уравнения циклоиды 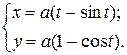
Одна арка задается изменением параметра 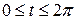 . Найдем производные координатных функций:
. Найдем производные координатных функций: 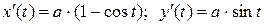 .
.
Упростим подынтегральное выражение в формуле для вычисления длины дуги
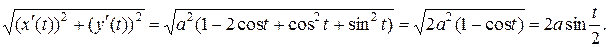
Подставляя в формулу и вычисляя интеграл, получаем:
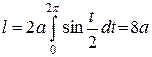 .
.
 2015-05-05
2015-05-05 1082
1082








