Рассмотрим случай, когда кривая задана в полярных координатах уравнением
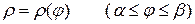 .
.
В этом случае в качестве параметра можно взять переменную 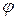 .
.
Найдем параметрические выражения для координатных функций.
Связь декартовых координат с полярными задается формулами

Известно, что длина дуги кривой, заданной параметрическими уравнениями, вычисляется по формуле 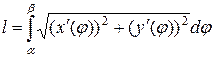 .
.
Вычислим производные координатных функций
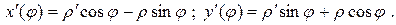
Подставим их в подкоренное выражение и упростим его
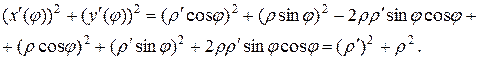
Подставляя это выражение в формулу длины дуги кривой, заданной параметрическими уравнениями, получаем формулу длины дуги, заданной
в полярных координатах
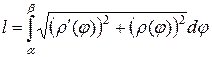 .
.
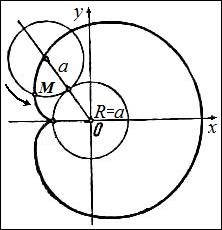 Пример. Пусть по внешней части колеса радиуса
Пример. Пусть по внешней части колеса радиуса 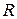 движется колесо меньшего радиуса
движется колесо меньшего радиуса 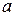 . Точка, зафиксированная на ободе колеса меньшего радиуса, будет описывать линию, называемую эпициклоидой.
. Точка, зафиксированная на ободе колеса меньшего радиуса, будет описывать линию, называемую эпициклоидой.
Если 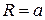 , то такая эпициклоида называется
, то такая эпициклоида называется
кардиоидой. Уравнение кардиоиды в полярных координатах 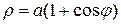 .
.
Так как кривая симметрична относительно оси OX, то можно найти длину 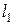 половины кривой, расположенную выше оси OX. Формула длины дуги в полярных координатах
половины кривой, расположенную выше оси OX. Формула длины дуги в полярных координатах
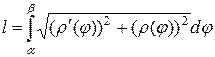 .
.
Вычислим производную 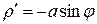 и упростим подкоренное выражение
и упростим подкоренное выражение
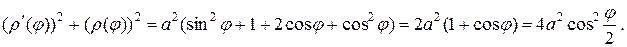
Подставляя в формулу, находим половину длины кривой
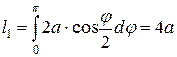 .
.
Тогда длина всей кардиоиды 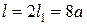 .
.
 2015-05-05
2015-05-05 11706
11706
