Рассмотрим часто встречающийся случай, когда плоская кривая задана явно уравнением 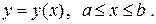 В этом случае можно в качестве параметра взять переменную
В этом случае можно в качестве параметра взять переменную 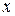 . Подставляя уравнения
. Подставляя уравнения 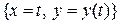 в формулу (8.1) длины дуги параметрически заданной кривой, и заменяя
в формулу (8.1) длины дуги параметрически заданной кривой, и заменяя 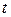 на
на 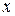 , получаем:
, получаем:
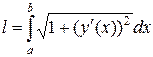
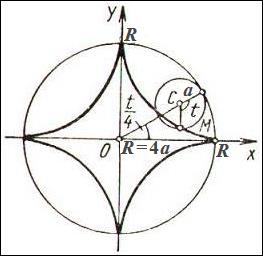
Пример. Пусть по внутренней частиобруча большого радиуса 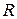 движется колесо меньшего радиуса
движется колесо меньшего радиуса 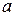 . Точка, отмеченная на ободе колеса меньшего радиуса, будет описывать линию, называемую гипоциклоидой. Если
. Точка, отмеченная на ободе колеса меньшего радиуса, будет описывать линию, называемую гипоциклоидой. Если 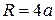 , то такая гипоциклоида называется астроидой. Уравнение астроиды
, то такая гипоциклоида называется астроидой. Уравнение астроиды 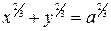 .
.
Найдем длину астроиды. Поскольку эта кривая симметрична относительно осей  и
и 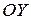 , то будем искать длину
, то будем искать длину 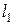 части кривой, находящейся в первой четверти. Она задается уравнением
части кривой, находящейся в первой четверти. Она задается уравнением 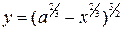 ,
, 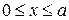 . Сделаем необходимые вычисления
. Сделаем необходимые вычисления
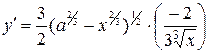 ;
; 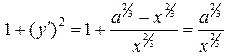 .
.
Подставив это выражение в формулу для вычисления длины дуги, найдем длину части кривой, лежащей в первой четверти
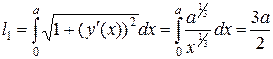 .
.
Длина всей астроиды 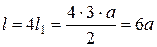 .
.
 2015-05-05
2015-05-05 1273
1273








