Плоская фигура D квадрируема тогда и только тогда, когда для любого сколь угодно малого 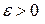 найдутся многоугольники
найдутся многоугольники 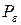 и
и 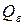 , такие, что
, такие, что 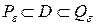 и
и 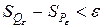 .
.
Доказательство.
Необходимость. Пусть фигура квадрируема, то есть 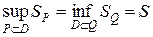 . Зафиксируем
. Зафиксируем 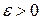 . По определению точной верхней грани для
. По определению точной верхней грани для 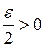 найдется вписанный многоугольник
найдется вписанный многоугольник 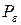 , такой, что
, такой, что 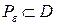 и
и 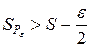 .
.
По определению точной нижней грани для 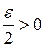 найдется описанный многоугольник
найдется описанный многоугольник 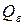 , такой, что
, такой, что 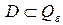 и
и 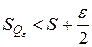 .
.
Тогда разность площадей описанного и вписанного многоугольников
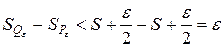 .
.
Достаточность. Пусть нашлись многоугольники 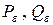 такие, что
такие, что 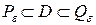 и
и 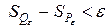 . Из определения точных верхней и нижней граней следует оценка
. Из определения точных верхней и нижней граней следует оценка 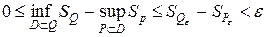 .
.
Так как 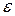 - сколь угодно мало, то
- сколь угодно мало, то 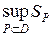 и
и 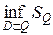 совпадают, следовательно, фигура квадрируема.
совпадают, следовательно, фигура квадрируема.
Теорема 1. Криволинейная трапеция, то есть фигура 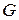 , ограниченная линиями
, ограниченная линиями 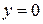 ,
, 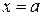 ,
, 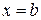 ,
, 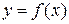 , где
, где  – непрерывна на отрезке
– непрерывна на отрезке  и
и 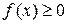 , является квадрируемой фигурой и ее площадь находится по формуле
, является квадрируемой фигурой и ее площадь находится по формуле 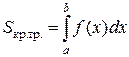 .
.
Доказательство. Зафиксируем 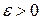 . Так как
. Так как  – непрерывна на отрезке
– непрерывна на отрезке  , то она интегрируема на этом отрезке и существует
, то она интегрируема на этом отрезке и существует 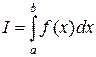 .
.
Тогда по критерию интегрируемости
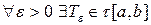 такое что
такое что 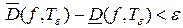 .
.
Величина верхней суммы Дарбу 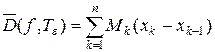 равна площади ступенчатой фигуры
равна площади ступенчатой фигуры 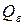 , описанной вокруг криволинейной трапеции G.
, описанной вокруг криволинейной трапеции G.
Величина нижней суммы Дарбу 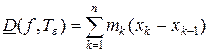 равна площади ступенчатой фигуры
равна площади ступенчатой фигуры 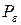 , вписанной в криволинейную трапецию G.
, вписанной в криволинейную трапецию G.
Так как нашли многоугольники 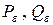 такие, что
такие, что 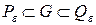 и
и 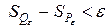 ,
,
то по критерию квадрируемости криволинейная трапеция G является квадрируемой фигурой.
Для оценки площади криволинейной трапеции справедливы неравенства
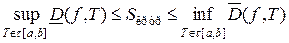 . Учитывая, что
. Учитывая, что 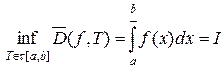 и
и 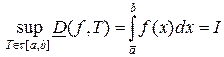 ,
,
получаем формулу 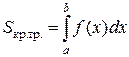 .
.
 2015-05-05
2015-05-05 4121
4121








