
Статическим моментом точки относительно оси называется произведение массы точки на расстояние до прямой.
Рассмотрим плоскую кривую, у которой плотность равна 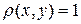 , тогда масса кривой равна ее длине, найдём статический момент кривой относительно оси
, тогда масса кривой равна ее длине, найдём статический момент кривой относительно оси  .
.
Пусть кривая задана уравнением 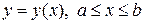 . Возьмем на кривой точку
. Возьмем на кривой точку 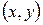 и вырежем из кривой элементарный участок длины
и вырежем из кривой элементарный участок длины 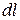 , содержащий точку
, содержащий точку 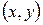 . Если считать массу участка, равную
. Если считать массу участка, равную 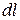 , сосредоточенной в точке
, сосредоточенной в точке 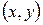 , то элементарный момент, то есть статический момент малого элемента кривой относительно оси
, то элементарный момент, то есть статический момент малого элемента кривой относительно оси  равен
равен 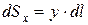 . Тогда статический момент всей кривой относительно оси
. Тогда статический момент всей кривой относительно оси  , находится по формуле
, находится по формуле 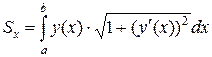 .
.
Аналогично выводится формула для вычисления статического момента кривой относительно оси 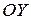 :
: 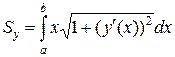 .
.
Определение. Центр тяжести кривой 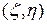 – это такая точка, что если в ней сосредоточить всю массу кривой, то ее статический момент относительно оси, не пересекающей кривую, будет равен статическому моменту всей кривой:
– это такая точка, что если в ней сосредоточить всю массу кривой, то ее статический момент относительно оси, не пересекающей кривую, будет равен статическому моменту всей кривой: 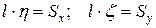 .
.
Отсюда получаем формулы для нахождения координат центра тяжести однородной кривой 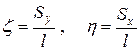 .
.
В случае если кривая задана явно уравнением 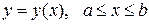 , координаты центра тяжести кривой находятся по формулам
, координаты центра тяжести кривой находятся по формулам
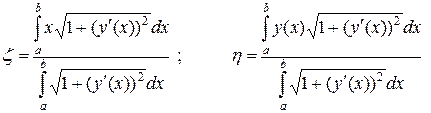 .
.
Пример 1. Найти статический момент полуокружности относительно её диаметра.
Расположим полуокружность так, чтобы её диаметр находился на оси  , а центр в начале координат.
, а центр в начале координат.
Уравнение верхней полуокружности 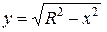 . Найдем значение подкоренного выражения в формуле для вычисления статистического момента
. Найдем значение подкоренного выражения в формуле для вычисления статистического момента 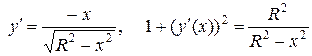 . Подставляя в формулу, получаем ответ
. Подставляя в формулу, получаем ответ 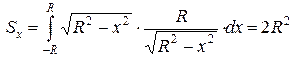 .
.
Пример 2. Найти статический момент относительно оси  и координаты центра тяжести дуги астроиды, расположенной в первой четверти.
и координаты центра тяжести дуги астроиды, расположенной в первой четверти.
Запишем параметрические уравнения астроиды
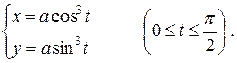
Формула для вычисления статического момента в случае, если кривая задана параметрическими уравнениями 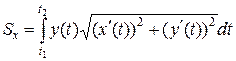 .
.
Вычислим подкоренное выражение
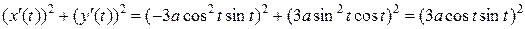 .
.
Подставив в формулу, находим значение статического момента
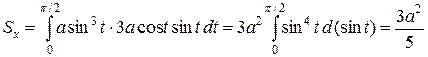 .
.
Найдем координаты центра тяжести 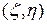 кривой.
кривой.
В силу симметрии 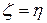 . Найдем ординату центра тяжести по формуле
. Найдем ординату центра тяжести по формуле
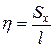 , где
, где 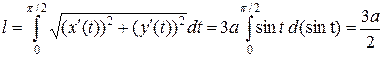 .
.
Отсюда 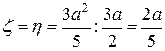 .
.
 2015-05-05
2015-05-05 13554
13554








