Рассматриваем случай, когда фигура является однородной, то есть ее плотность в каждой точке равна 1. Пусть фигура является криволинейной трапецией, ограниченной сверху графиком функции 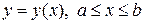 . Выделим элементарную бесконечно узкую вертикальную полоску. Приняв эту полоску приближенно за прямоугольник, находим ее массу, равную площади
. Выделим элементарную бесконечно узкую вертикальную полоску. Приняв эту полоску приближенно за прямоугольник, находим ее массу, равную площади 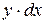 . Для определения соответствующих элементарных моментов предположим всю массу полоски сосредоточенной в ее центре тяжести, то есть центре прямоугольника. Полученная материальная точка отстоит от оси
. Для определения соответствующих элементарных моментов предположим всю массу полоски сосредоточенной в ее центре тяжести, то есть центре прямоугольника. Полученная материальная точка отстоит от оси  на расстояние
на расстояние 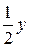 , от оси
, от оси 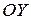 на расстояние
на расстояние 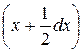 , что приближенно равно
, что приближенно равно 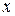 . Тогда элементарные моменты равны
. Тогда элементарные моменты равны 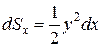 и
и 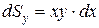 . Отсюда получаем формулы
. Отсюда получаем формулы
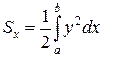 ;
; 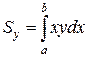 .
.
Координаты центра тяжести 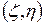 однородной криволинейной трапеции определяются по формулам
однородной криволинейной трапеции определяются по формулам 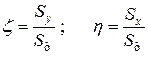 .
.
В случае явного задания функции уравнением 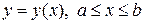 , имеем
, имеем
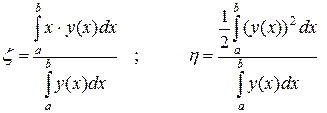 .
.
Пример 3. Найти статический момент относительно оси  и координаты центра тяжести фигуры ограниченной осью
и координаты центра тяжести фигуры ограниченной осью  и одной аркой циклоиды.
и одной аркой циклоиды.
Запишем параметрические уравнения циклоиды
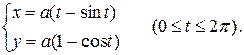
Подставим эти уравнения в формулу для вычисления статического момента фигуры относительно оси  :
:
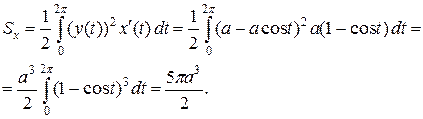
Найдем координаты центра тяжести фигуры. Так как  , то фигура симметрична относительно прямой
, то фигура симметрична относительно прямой 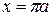 . Поэтому абсцисса центра тяжести
. Поэтому абсцисса центра тяжести 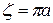 . Ординату центра тяжести находим по формуле
. Ординату центра тяжести находим по формуле 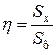 .
.
Вычислим площадь фигуры
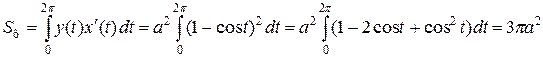 .
.
Учитывая, что соответствующий статический момент уже посчитан, находим ординату центра тяжести 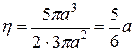 . Итак, центр тяжести фигуры расположен в точке
. Итак, центр тяжести фигуры расположен в точке 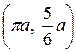 .
.
 2015-05-05
2015-05-05 2963
2963
