Пусть функция 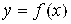 непрерывна на конечном промежутке
непрерывна на конечном промежутке 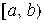 , но не ограничена на этом промежутке.
, но не ограничена на этом промежутке.
Определение. Несобственным интегралом 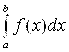 от функции у=f(x) на промежутке
от функции у=f(x) на промежутке  называется предел
называется предел 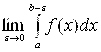 , т.е.
, т.е.
 . (15)
. (15)
Если предел, стоящий в правой части равенства (15) существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
Интеграл (15) иногда называют несобственным интегралом второго рода.
Аналогично вводится понятие несобственного интеграла от функции 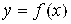 непрерывной, но не ограниченной на промежутке
непрерывной, но не ограниченной на промежутке 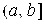 :
:
 . (16)
. (16)
Если функция 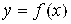 не ограничена при
не ограничена при 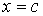 , где
, где 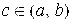 , и непрерывна при
, и непрерывна при 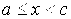 и
и 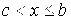 , то несобственный интеграл от функции у=f(x) на отрезке
, то несобственный интеграл от функции у=f(x) на отрезке  обозначается
обозначается  и определяется равенством
и определяется равенством
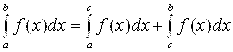 . (17)
. (17)
Несобственный интеграл (17) называется сходящимся, если сходятся оба несобственных интеграла в правой части равенства (17).
В противном случае данный интеграл называется расходящимся.
Пример 17. Исследовать на сходимость несобственные интегралы:
а) 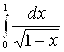 ; б)
; б) 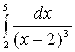 .
.
Решение: а) данный интеграл является интегралом от неограниченной функции (подынтегральная функция  не определена в точке
не определена в точке 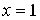 , при
, при 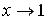 эта функция неограниченно возрастает).
эта функция неограниченно возрастает).
По определению имеем
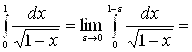 [замена:
[замена: 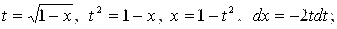
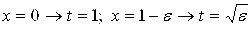 ] =
] = 
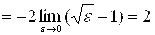 , следовательно, данный интеграл сходится.
, следовательно, данный интеграл сходится.
б) по определению
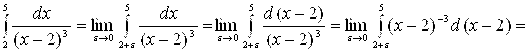

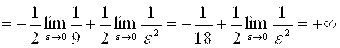 .
.
Значит, данный интеграл является расходящимся.
 2015-05-05
2015-05-05 8001
8001
