При введении понятия определённого интеграла 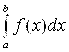 предполагалось, что выполняются следующие два условия:
предполагалось, что выполняются следующие два условия:
а) пределы интегрирования а и 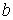 являются конечными;
являются конечными;
б) подынтегральная функция 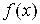 ограничена на отрезке
ограничена на отрезке 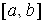 .
.
Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.
Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.
Определение. Пусть функция 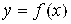 определена и непрерывна на промежутке
определена и непрерывна на промежутке 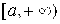 , тогда
, тогда
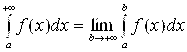 (12)
(12)
называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).
Если 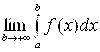 существует и конечен, то несобственный интеграл
существует и конечен, то несобственный интеграл 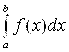 называется сходящимся; если данный предел не существует или равен
называется сходящимся; если данный предел не существует или равен 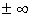 , то несобственный интеграл называется расходящимся.
, то несобственный интеграл называется расходящимся.
Геометрически несобственный интеграл  от неотрицательной функции
от неотрицательной функции 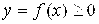 выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции
выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции 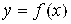 , снизу – осью
, снизу – осью  , слева – отрезком прямой
, слева – отрезком прямой 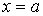 и неограниченной справа (рис. 15).
и неограниченной справа (рис. 15).
Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.
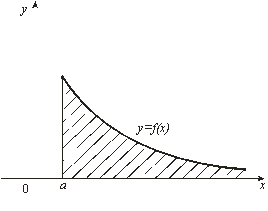
Рис. 15
Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:
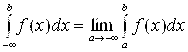 . (13)
. (13)
Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:
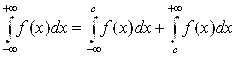 , (14)
, (14)
где с – любая точка интервала 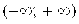 . Интеграл
. Интеграл  сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).
сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).
Пример 16. Исследовать на сходимость несобственные интегралы:
а) 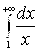 ; б)
; б) 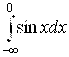 ; в)
; в) 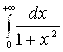 ; г)
; г)  .
.
Решение. а) 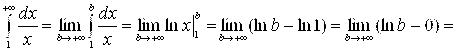
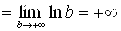 , следовательно, данный интеграл расходится;
, следовательно, данный интеграл расходится;
б) 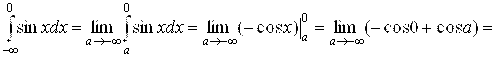
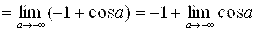 . Так как при
. Так как при 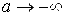 предел
предел 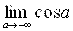 не существует, то интеграл
не существует, то интеграл 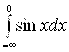 расходится;
расходится;
в) 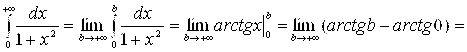
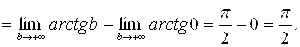 Значит, несобственный интеграл
Значит, несобственный интеграл 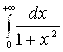 сходится и его значение равно
сходится и его значение равно 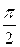 ;
;
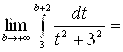
г) 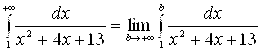 = [выделим в знаменателе полный квадрат:
= [выделим в знаменателе полный квадрат: 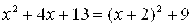 ] =
] = 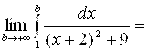 [замена:
[замена: 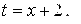
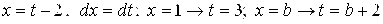 ] =
] = 

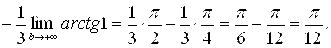
Значит, несобственный интеграл сходится и его значение равно 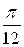 .
.
 2015-05-05
2015-05-05 13085
13085








