Запишем расширенную матрицу системы и, используя элементарные преобразования, приведем ее к трапециевидной форме:


Ранг матрицы основной системы равен рангу расширенной системы и равен трем. Символически это можно записать так: 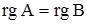 .
.
Число неизвестных равно четырем, следовательно, три неизвестные – базисные, одно – свободное. Базисный минор:
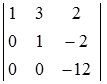
состоит из коэффициентов при неизвестных х1, х2 и х3, следовательно, именно они – базисные, а х4 – свободный. Пусть х4 = a – произвольное число.
Из последней строки преобразованной матрицы получим:
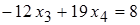 .
.
Откуда
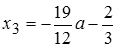
или
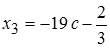 ,
,
где 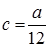 – также произвольное число.
– также произвольное число.
Аналогично из второй строчки преобразованной матрицы получим:
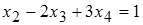 .
.
Подставим значения х3 и х4 и определим значение х2:
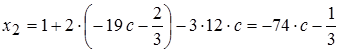 .
.
Из первой строчки преобразованной матрицы получим:
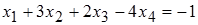
или
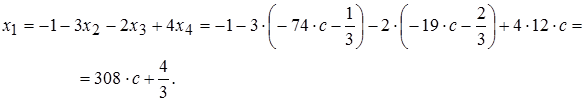
Ответ: Общее решение системы имеет вид:
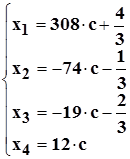 .
.
 2015-05-05
2015-05-05 791
791







