Параллельность прямой и плоскости

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Для обозначения параллельности используется символ «». То есть, если прямая a и плоскость α параллельны, то можно кратко записать a α. (рис.10)

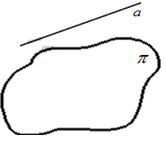
Рис.10

В качестве примера параллельных прямой и плоскости приведем натянутую гитарную струну и плоскость грифа этой гитары.

Параллельность прямой и плоскости далеко не всегда является очевидным фактом. Другими словами, параллельность прямой и плоскости приходится доказывать. Существует достаточное условие, выполнение которого гарантирует параллельность прямой и плоскости. Это условие называют признаком параллельности прямой и плоскости.

Теорема 2.6. Если прямая a, не лежащая в плоскости α, параллельна некоторой прямой a₁, которая лежит в плоскости α, то прямая a параллельна плоскости α (рис.11)

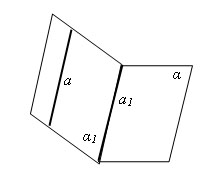
Рис.11