Основные классы случайных процессов

1) Процессы с независимыми приращениями

ОПР: Процесс x(t) называется процессом с независимыми приращениями, если для

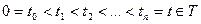" возрастающих моментов времени СВ приращения:

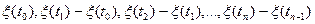- являются нез.

Примеры: пуассоновский и броуновский процессы

2) Марковские процессы

ОПР: s-алгеброй прошлого к моменту времени t называется s-алгебра: =: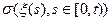

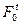
где x(s), s Î [0,T] - процесс

ОПР: s-алгебра настоящего - s-алгебра, порожденная СВ x(t): s(x(t)) =: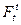

ОПР: s-алгебра будущего - s-алгебра: =: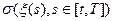

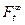
ОПР: СП x(t) называется марковским, если для " настоящего момента времени t и

" множеств А 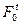Î и В Î 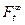: 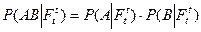- условная независимость

прошлого от будущего (при условии настоящего)

3) Мартингалы

Свойства условного мат.ожидания (отн-но s-алгебры А): 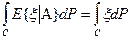, x - А-изм., СÎА

1) линейность: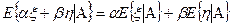

2) пусть x не зависит от А (" измеримая отн-но А – СВ h - не зависит от x):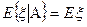

3) пусть x, h - СВ и x измеримо отн-но А: 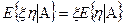Þ 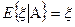при h º 1

4) есть две s-алгебры M Ì A Ì F, (M - более бедная): E {x½M } = E { E {x½A}½M }

(W,F, Р), 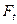- возрастающий поток s-алгебр, в любой момент времени s < t, s, t Î T: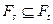

ОПР: x(t), t Î T называется мартингалом, если

(1) конечность моментов + согласованность: " t 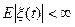, процесс x(t) - 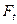измерим

(2) " s < t, где s, t Î T 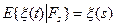п.н. (с вер-тью 1) – усредняя значение процесса в будущем отн-но некоторой s-алгебры прошлого, получаем значение процесса в прошлом.

ОПР: x(t), t Î T называется субмартингалом, если

(1) конечность моментов + согласованность

(2) " s < t, где s, t Î T 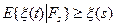п.н. (с вероятностью 1)

ОПР: x(t), t Î T называется супермартингалом, если

(1) конечность моментов + согласованность

(2) " s < t, где s, t Î T 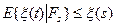п.н. (с вероятностью 1)

Примеры: - мартингал – сумма н.о.р. СВ с 0-ым м/о,

- субмартингал – квадрат суммы н.о.р. СВ с 0-ым м/о

4) Гауссовские случайные процессы

ОПР: процесс x(t), t Î T называется гауссовским, если все его КМР есть гауссовские, т.е.

случайный вектор 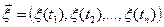, 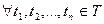- гауссовские

УТВ: процесс называется гауссовским, если линейные комбинации любых его наборов есть одномерные гауссовские величины.

УТВ: гауссовские величины выдерживают предельный переход: интеграл от гауссовского процесса – есть гауссовский процесс.

5) Стационарные случайные процессы

ОПР: процесс x(t), t Î T – стационарный в узком смысле, если его КМР не зависят от сдвига параметра, не выходящего за пределы параметрического множества, т.е:

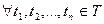и " t: 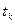+ t Î T ® 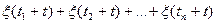- не зависят от t.

Характеристики СП:

(1) независимость от сдвига (МО не зависит от времени): 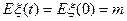- const

(2) функция ковариаций зависит только отразности: R(s, t) = R(t - s)

ОПР: процесс x(t), t Î T – стационарный в широком смысле, если

(1) " t Î T - конечны дисперсии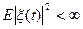

(2) выполнены (1) и (2) выше (см. характеристики СП)