Рассматрим теорию мартингалов с дискретным временем.
ОПР: последовательность 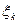 - супермартингал, т.е.: " k < n
- супермартингал, т.е.: " k < n 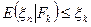 (1)
(1)
Применим мат. ожидание к неравенству (1) и получим: 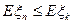 (2)
(2)
Супермартингальное неравенство: " k < n, 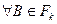 :
: 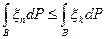 (3) – при этом (1) Û (3)
(3) – при этом (1) Û (3)
Теорема (Т.Дуба о преобразовании свободного выбора)
Последовательность 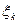 , k = 1,2,…, n – супермартингал относительно потока s-алгебр
, k = 1,2,…, n – супермартингал относительно потока s-алгебр 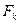
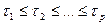 ,
, 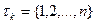 ,
, 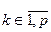 - моменты остановки (упорядоченные) отн-но
- моменты остановки (упорядоченные) отн-но 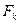
Тогда последовательность 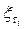 ,
, 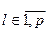 - супермартингал относительно потока s-алгебр
- супермартингал относительно потока s-алгебр 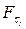
 2015-05-05
2015-05-05 1081
1081








