Теорема (А.Н.Колмогорова) (б.док-ва) о непрерывности траекторий

ОПР: говорят, что процесс x(t), t Î T – стохастически непрерывен в (×) 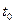, если

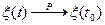по вероятности при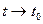

Напоминание: сходимость по вероятности: , ,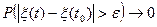

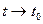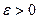
ОПР: процесс x(t), t Î T – стохастически непрерывен, если он стох. непрерывен в "(×) 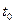Î T

ОПР: процесс x(t), t Î T – непрерывен, если все его траектории непрерывны с вероятностью 1.

Теорема (Колмогорова о непрерывности процесса):

Пусть для процесса x(t), t Î [ a, b ] выполняется условие Колмогорова:

$ const K,a,b > 0: " s < t, где s, t Î [ a, b ] верно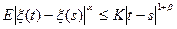

Тогда у x(t) $ непрерывная модификация 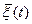, траектории которой обладают свойством:

" s < t выполняется 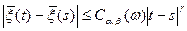, , 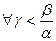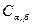- случайная const

Пример: свойство траекторий броуновского движения – они непрерывны, но нигде не дифференцируются.