Теорема (1-ое тождество Вальда):
Пусть 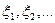 - последовательность нез.о.р. СВ,
- последовательность нез.о.р. СВ, 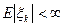
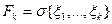 - поток s-алгебр, порожденный СВ
- поток s-алгебр, порожденный СВ 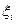 , i = 1,2,…, k
, i = 1,2,…, k
t - момент остановки относительно 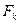 : t Î N
: t Î N
Тогда 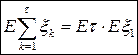 (верхн. индекс суммирования случайный – это момент остановки)
(верхн. индекс суммирования случайный – это момент остановки)
Теорема (2-ое тождество Вальда):
Пусть 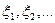 - последовательность нез.о.р. СВ,
- последовательность нез.о.р. СВ, 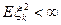
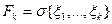 - поток s-алгебр, порожденный СВ
- поток s-алгебр, порожденный СВ 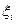 , i = 1,2,…, k
, i = 1,2,…, k
t - момент остановки относительно 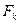 : t Î N
: t Î N
Тогда 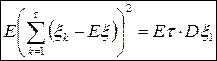
Теорема (фундаментальное тождество Вальда):
Пусть 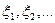 - последовательность нез.о.р. СВ,
- последовательность нез.о.р. СВ, 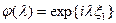 - хар. функция
- хар. функция
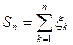 - частичная сумма
- частичная сумма
t - момент остановки относительно 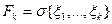
Тогда 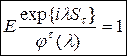
9. Т-ма о числе пересечений субмартингалом полосы (a, b). Теорема (Дуба) о сходимости субмартингалов.
Интервал [ a, b ] рассмотренный во времени
Последовательность 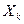 , k = 1,2,…, где
, k = 1,2,…, где 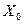 = 0, а
= 0, а 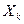 -
- 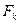 -измеримо
-измеримо
Есть дискретные моменты времени, определим моменты остановки: пусть 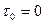 , а
, а
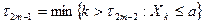 - до пересечения уровня «a»
- до пересечения уровня «a»
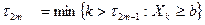 - после пересечения уровня «b»
- после пересечения уровня «b»
Определим величину: 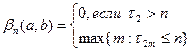
Пара моментов с нечетн. и четн. индексом называется пересечением полосы (a, b), а 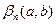 - число пересечений снизу вверх полосы (a, b) последовательностью
- число пересечений снизу вверх полосы (a, b) последовательностью 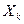 до момента времени n.
до момента времени n.
Теорема (Т. Дуба о числе пересечений): пусть 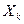 - субмартингал отн-но потока
- субмартингал отн-но потока 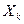 Þ
Þ
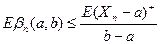 , где
, где 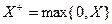 ,
, 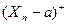 - превышение уровня «a»
- превышение уровня «a»
Теорема (Т. Дуба о сходимости субмартингалов):
пусть (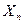 ,
, 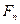 ) – субмартингал,
) – субмартингал, 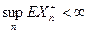 Þ
Þ 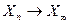 п.н. (с вер. 1) и
п.н. (с вер. 1) и 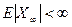
Следствия:
1) пусть 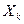 £ 0 – неположительный субмартингал сходится с вер-тью 1
£ 0 – неположительный субмартингал сходится с вер-тью 1
2) пусть 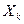 ³ 0 – нетрицательный мартингал сходится с вер-тью 1
³ 0 – нетрицательный мартингал сходится с вер-тью 1
Лемма Бореля-Кантелли:
Пусть 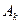 , k = 1,2,… - последовательность событий: ряд
, k = 1,2,… - последовательность событий: ряд 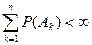
Тогда с вер-тью 1 $ 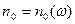 : " n >
: " n > 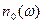 наступает
наступает 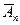
 2015-05-05
2015-05-05 1688
1688








