Теорема о существовании и единственности решений стохастического дифференциального уравнения

Теорема (о $ и! решения стохастических уравнений)

Пусть коэффициенты а и d удовлетворяют:

1) для 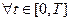, 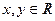: удовлетворяют условию Липшица с показателем 1

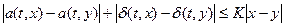
2) выполняется условие на не более, чем линейный рост: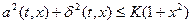

Начальные условия:

1) 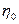- не зависит от приращения броуновского движения вперед: ,

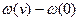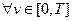
2)

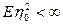
Тогда у уравнения 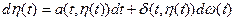$ с вер-тью 1 непрерывное решение:

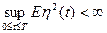
и решение 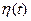с такими свойствами единственно.