ОПР (Колмогоров): марковский процесс 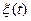 ,
, 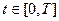 называется диффузионным, если его переходная вероятность
называется диффузионным, если его переходная вероятность 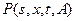 (непрерывно по x) удовлетворяет условиям, s < t:
(непрерывно по x) удовлетворяет условиям, s < t:
1) "e > 0 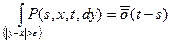
2) $e > 0, функция a (s, x) - коэффициент сноса 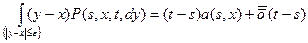
3) $e > 0, функция b (s, x) - коэффициент диф. 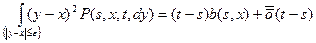
Достаточные условия диффузионности:
1¢) $ d>0: 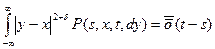 - вер.эквивалент:
- вер.эквивалент: 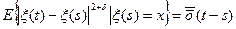
2¢) $ a (s, x): 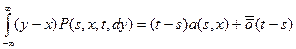 - вер. эквивалент аналогично
- вер. эквивалент аналогично
3¢) $ b (s, x): 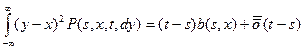 - вер. эквивалент аналогично
- вер. эквивалент аналогично
Лемма (обобщенная лемма Фубини):
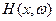 - ограниченная измеримая случайная функция, измеримая отн-но B ´ F, x Î
- ограниченная измеримая случайная функция, измеримая отн-но B ´ F, x Î 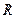 ,
, 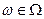
и пусть 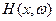 как процесс не зависит от s-алгебры А Î F:
как процесс не зависит от s-алгебры А Î F: 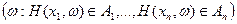
т.е. праобразы любого момента времени не зависят от s-алгебры А и пусть СВ x - А -измерима
Тогда 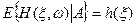 п.н. (т.е. кроме множества меры 0), где
п.н. (т.е. кроме множества меры 0), где 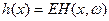
 2015-05-05
2015-05-05 464
464








