Броуновское движение: 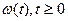 , пусть
, пусть 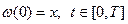
Процесс с нез. приращениями: 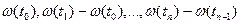 ,
, 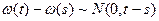
1) 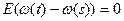
2) 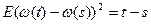
Пусть $ поток s-алгебры 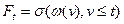 : " t
: " t 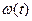 -
- 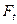 -измеримо
-измеримо
Независимость приращений вперед: для " 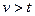 -
- 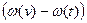 - не зависим от
- не зависим от 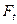
Опишем класс подынтегральных функций, для которых Ито строил интегралы: 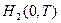
1) 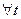 ,
, 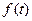 -
- 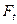 -измерим (т.е. согласованность с потоком)
-измерим (т.е. согласованность с потоком)
2) 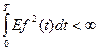
Речь идет о пространствах 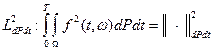 - квадрат нормы по мере произведения (вероятностная мера ´ мера Лебега).
- квадрат нормы по мере произведения (вероятностная мера ´ мера Лебега).
Интеграл должен отвечать требованиям:
1) линейность: 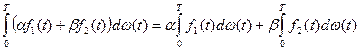
2) 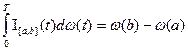
3) 1. 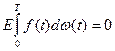
2. 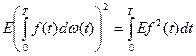 - изометрия, совпадение норм
- изометрия, совпадение норм
Разобъем [0,T] на интервалы: 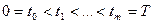 и определим ступенчатые функции:
и определим ступенчатые функции:
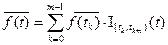 - при этом
- при этом 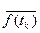 -
- 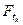 -измерима
-измерима
Будем аппроксимировать 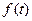 только в левом конце.
только в левом конце.
ОПР: Стохастический интеграл для ступенч. функций: 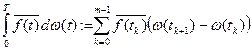
Лемма: для " f Î 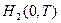 $ последовательность ступ.функций
$ последовательность ступ.функций 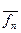 Î
Î 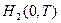 :
:
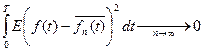
т.е. $ последовательность ступ.функций, которые аппроксимируют f.
Для " аппр.посл-ти предел будет один и тот же. Этот предел I (Т) называется стохастическим интегралом подынтегральной функции 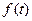 Î
Î 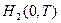 :
: 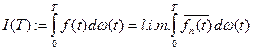
 2015-05-05
2015-05-05 401
401








