1°. 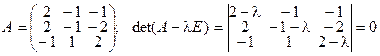 . Корни характеристического уравнения: l1, 2, 3 = 1.
. Корни характеристического уравнения: l1, 2, 3 = 1. 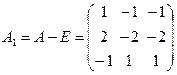 .
.
Собственные векторы А по λ = 1, т.е. ядро А 1:
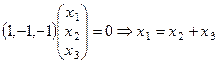 , значит базис N (А 1):
, значит базис N (А 1): 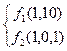 .
.
Образ оператора А 1 М (А 1) находим из соотношений:
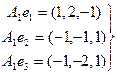 ; базис М (А 1) f 3(1, 2, –1), и т.к. f 3 = 2 f 1 – f 2, то f 3Îℒ(f 1, f 2).
; базис М (А 1) f 3(1, 2, –1), и т.к. f 3 = 2 f 1 – f 2, то f 3Îℒ(f 1, f 2).
Тогда: базисом 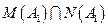 будет вектор
будет вектор 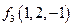 ; вектором, дополняющим базис
; вектором, дополняющим базис 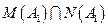 до базиса
до базиса 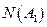 будет любой из векторов
будет любой из векторов 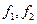 , например вектор
, например вектор 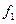 ; а базис
; а базис 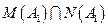 дополнить до базиса
дополнить до базиса 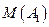 нечем, т.к.
нечем, т.к. 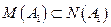 .
.
Прообраз А 1 у = (1, 2, –1) Þ у 1 – у 2 – у 3 = 1, например (1, 0, 0).
Кстати: система А 1 у = (1, 0, 0) решений не имеет, т.е. прообраза второго слоя для вектора (1, 2, –1) нет.
Следовательно, жорданов базис оператора А: 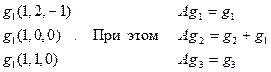 .
.
И, окончательно, имеем жорданову форму матрицы оператора А: 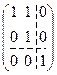 .
.
2°. Найти нормальную жорданову форму матрицы линейного оператора А = 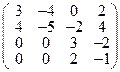 и базис, в котором матрица оператора имеет жорданову форму.
и базис, в котором матрица оператора имеет жорданову форму.
Δ. Для матрицы линейного оператора А = 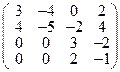 составим и решим характеристическое уравнение: det(A - l E) = 0.
составим и решим характеристическое уравнение: det(A - l E) = 0.
Получим:
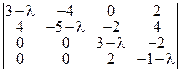 =
= 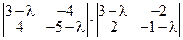 .
.
Тогда:  = 0 и, следовательно, l1, 2 = –1; l3, 4 = 1.
= 0 и, следовательно, l1, 2 = –1; l3, 4 = 1.
a) Рассмотрим оператор А -1 = А -l E = А + E = 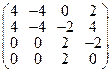 . Ищем собственные векторы оператора А при l = - 1, т. е. ядро оператора А -1. Для этого решим систему четырех линейных однородных уравнений с матрицей А -1. Из третьего и четвертого уравнений системы видно, что
. Ищем собственные векторы оператора А при l = - 1, т. е. ядро оператора А -1. Для этого решим систему четырех линейных однородных уравнений с матрицей А -1. Из третьего и четвертого уравнений системы видно, что 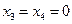 . Тогда можно легко установить, что
. Тогда можно легко установить, что 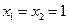 . Вектор f 1 (1, 1, 0, 0) - единственный собственный вектор оператора А, соответствующий собственному значению l = -1 и образует базис ядра оператора А –1. Далее ищем базис образа оператора А –1:
. Вектор f 1 (1, 1, 0, 0) - единственный собственный вектор оператора А, соответствующий собственному значению l = -1 и образует базис ядра оператора А –1. Далее ищем базис образа оператора А –1:
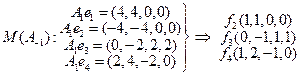 .
.
Отметив, что для векторов f 2, f 3, f 4 существует соотношение: f 3 + f 4 – f 2 = (0, 0, 0, 1), находим базис образа оператора А –1:
{j1 (1, 1, 0, 0), j2 (0, –1, 1, 1), j3 (0, 0, 0, 1).
Отметив, что векторы f 1 и 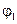 совпадают, делаем вывод о том, что этот вектор образует базис пересечения образа и ядра оператора А -1.
совпадают, делаем вывод о том, что этот вектор образует базис пересечения образа и ядра оператора А -1.
Кратность корня λ = -1 равна двум, а собственный вектор, соответствующий этому собственному значению, только один. Поэтому, полагаем g 1 равным вектору 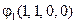 , а еще один вектор жорданового базиса ищем, как прообраз первого слоя для
, а еще один вектор жорданового базиса ищем, как прообраз первого слоя для 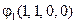 . Решаем неоднородную систему линейных уравнений
. Решаем неоднородную систему линейных уравнений 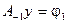 и находим второй вектор g 2(1, 3/4, 0, 0) жорданового базиса, соответствующего собственному значению l = -1 кратности два. При этом, что характерно, у вектора
и находим второй вектор g 2(1, 3/4, 0, 0) жорданового базиса, соответствующего собственному значению l = -1 кратности два. При этом, что характерно, у вектора 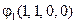 нет прообраза второго слоя, ибо система
нет прообраза второго слоя, ибо система 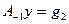 с расширенной матрицей
с расширенной матрицей
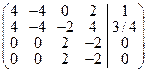
решений не имеет. Это и не случайно, потому что собственному значению l= -1 кратности 2 должно соответствует два вектора жорданового базиса оператора А:
g 1(1, 1, 0, 0); g 2(1, 3/4, 0, 0).
При этом отметим, что:
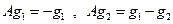 .
.
б) Теперь рассмотрим собственное значение l = 1 и, соответственно, оператор А 1= А + Е:
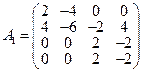 .
.
Найдем ядро этого оператора, т.е. собственные векторы оператора А при λ = 1.
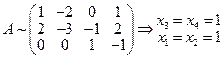 .
.
Вектор f 1 (1, 1, 1, 1) образует базис ядра оператора А 1 и является единственным собственным вектором оператора А, отвечающим собственному значению l = 1.
Ищем базис образа М (А 1) оператора А 1 .
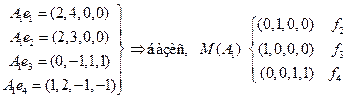 .
.
Отмечая, что f 1 = f 2 + f 3 + f 4, заключаем: базисом пересечения ядра и образа оператора A 1 является вектор f 1.
Так как собственный вектор только один, а собственное значение имеет кратность 2, требуется найти еще один вектор жорданового базиса. Поэтому полагаем g 3 равным вектору y1(1, 1, 1, 1), а еще один вектор жорданового базиса ищем как прообраз первого слоя для y1(1, 1, 1, 1). Для этого решаем неоднородную систему линейных уравнений A 1 g 4 = j1 и находим вектор g 4(0, 1/2, 0, 1/2) жорданового базиса, соответствующего собственному значению l = 1 кратности два. При этом у вектора y1(1, 1, 1, 1) нет прообраза второго слоя, ибо система A 1 y = g 4 с расширенной матрицей 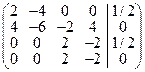 решений не имеет. И вновь это не случайно, потому что собственному значению l= 1 кратности 2 должно соответствовать два вектора жорданового базиса, а они уже найдены:
решений не имеет. И вновь это не случайно, потому что собственному значению l= 1 кратности 2 должно соответствовать два вектора жорданового базиса, а они уже найдены:
g 3(1, 1, 1, 1); g 4(0, 1/2, 0, 1/2).
При этом отметим, что: Ag 3 = g 1, Ag 4 = g 3 + g 4. Для оператора А найден жорданов базис: 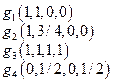 . При этом
. При этом 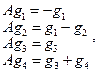 А G =
А G = 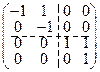 . ▲
. ▲
3°. 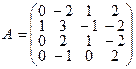 ; det(A - l E) = 0
; det(A - l E) = 0 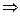 l1, 2 = 1; l3, 4 = 2.
l1, 2 = 1; l3, 4 = 2.
Δ a) Рассмотрим оператор А 1: А 1- E = 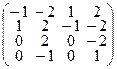 . Ищем собственные векторы оператора А при l = 1, т.е. ядро оператора А 1.
. Ищем собственные векторы оператора А при l = 1, т.е. ядро оператора А 1.
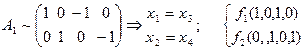 . Векторы { f 1, f 2} образуют базис N (A 1).
. Векторы { f 1, f 2} образуют базис N (A 1).
Далее ищем базис 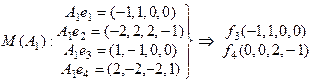 .
.
Так как векторы f 1, f 2, f 3, f 4 – линейно независимы, то 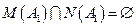 , а векторы дополняющие базис
, а векторы дополняющие базис 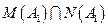 до базиса
до базиса 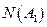 – векторы
– векторы 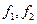 :
:
Кратность корня λ = 1 равна двум, поэтому имеем уже два вектора жорданового базиса А:
g 1(1, 0, 1, 0); g 2(0, 1, 0, 1).
б)Рассмотрим оператор А 2= А -2 Е: 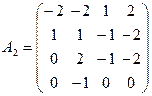 , и найдем ядро оператора А 2 т.е. собственные вектора А при λ = 2.
, и найдем ядро оператора А 2 т.е. собственные вектора А при λ = 2. 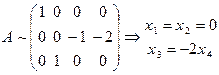 . Вектор f 1(0, 0, –2, 1), являющийся решением этой системы является одновременно и базисом ядра
. Вектор f 1(0, 0, –2, 1), являющийся решением этой системы является одновременно и базисом ядра 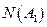 .
.
Ищем базис образа оператора А 2 – М (А 2).
 Þ
Þ 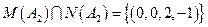 .
.
Тогда, вектор (0, 0, –2, 1) это вектор жорданового базиса, а второй вектор – прообраз вектора (0, 0, –2, 1), если он есть. Система для его нахождения: А 2 у = (0, 0, –2, 1).
Решаем систему А 2 у = (0, 0, –2, 1), для нахождения прообраза 1-го слоя вектора (0, 0, –2, 1) Получаем: 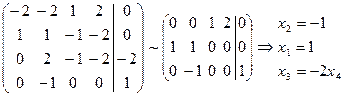 .
.
Решением системы является, например, вектор (1, –1, 0, 0).
Тогда g 3(0, 0, –2, 1); g 4(1, 1, 0, 0).
Для оператора А найден жорданов базис: 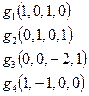 .
.
При этом 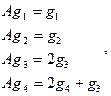 т.е. жорданова форма оператора А:
т.е. жорданова форма оператора А:  . ▲.
. ▲.
 2015-05-05
2015-05-05 4838
4838








