Дифференциальное уравнение вынужденных колебаний с учётом сопротивления
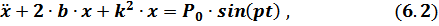
где 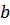 – коэффициент сопротивления среды,
– коэффициент сопротивления среды,
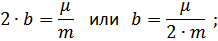
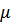 – коэффициент пропорциональности в выражении силы сопротивления
– коэффициент пропорциональности в выражении силы сопротивления
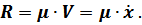
Решение дифференциального уравнения вынужденных колебаний с учётом сопротивления, как и прежде, состоит из двух частей
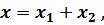
где 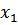 – общее решение уравнения
– общее решение уравнения 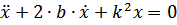 .
.
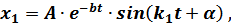
здесь
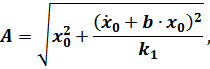
при 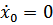 и с учётом, что
и с учётом, что 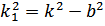
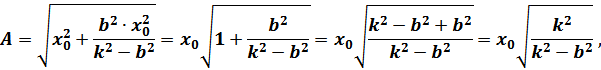
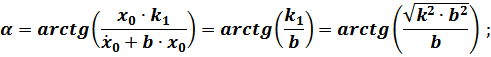
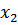 – частное решение, которое ищется в виде
– частное решение, которое ищется в виде
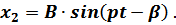
Здесь после преобразований получаются выражения для 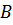 и
и 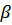
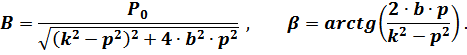
В итоге решение исходного дифференциального уравнения (6.2):
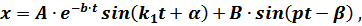
где при 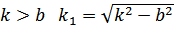 .
.
Величины 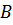 и
и 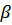 от начальных условий не зависят. Амплитуда
от начальных условий не зависят. Амплитуда 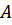 собственных колебаний за счёт множителя
собственных колебаний за счёт множителя 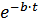 с течением времени уменьшается (рис. 6). Если принять в конце
с течением времени уменьшается (рис. 6). Если принять в конце 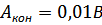 , то получаем расчётную формулу для времени установления вынужденных колебаний
, то получаем расчётную формулу для времени установления вынужденных колебаний
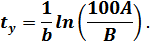
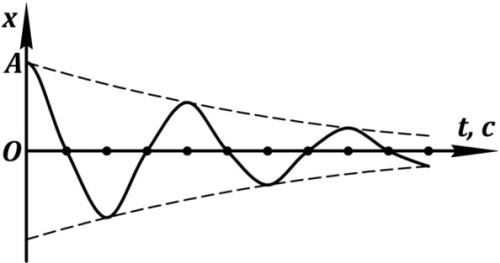
Рис. 6. График вынужденных колебаний
материальной точки с учётом сопротивления
По истечении времени 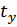 колебания становятся только вынужденными по закону
колебания становятся только вынужденными по закону
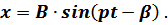
 2015-05-06
2015-05-06 340
340








