Автокорреляция первого, второго порядков

При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней 2-х или более рядов динамики различного содержания, но связанных между собой. Эта задача решается методами коррелирования:

· уровней ряда динамики

· отклонений фактических уровней от тренда

· последовательных разностей

Коррелирование уровней динамических рядов с применением парного коэффициента корреляции правильно показывает тесноту связи лишь в том случае, если в каждом из них отсутствует автокорреляция. Наличие зависимости между последующими и предшествую­щими уровнями динамического ряда в статистической литерату­ре называютавтокорреляцией [5].

Поэтому прежде, чем коррелировать ряды динамики по уровням, необходимо проверить каждый из рядов на наличие или отсутствие в них автокорреляции. Применение методов классической теории корреляции в ди­намических рядах связано с некоторыми особенностями. Преж­де всего, это наличие для большинства динамических рядов зави­симости последующих уровней от предыдущих.

Коэффициент автокорреляции вычисляется по непосред­ственным данным рядов динамики, когда фактические уровни од­ного ряда рассматриваются как значения факторного признака, а уровни этого же ряда со сдвигом на один период, принимаются в качестве результативного признака (этот сдвиг называется лагом). Коэффициент автокорреляции рассчитывается на основе фор­мулы коэффициента корреляции для парной зависимости:

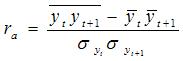
где:

· y_t– фактические уровни ряда,

· y_t+1 – уровни того же ряда со сдвигом на 1 период (коэффициент автокорреляции первого порядка).

Формула для расчета коэффициента автокорреляции уровней ряда 1-го порядка [2]:

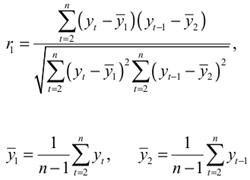
Формула для расчета коэффициента автокорреляции уровней ряда 2-го порядка [3]:

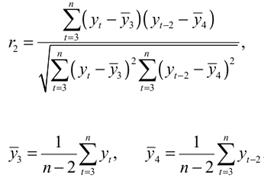
Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду, фактическое значение коэффициента автокорреляции сопоставляют с табличным для 5% или 1% уровня значимости. Если расчетное значение меньше табличного, то гипотеза об отсутствии автокорреляции принимается и, наоборот, в противном случае, отвергается.

Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции) называют коррелограммой [5].

Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т. е. определить присутствие в ряде той или иной компоненты. Так, если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка m, то ряд содержит циклические колебания с периодичностью в m моментов времени. Если же ни один из коэффициентов автокорреляции не является значимым, то можно сделать одно из двух предположений:

· либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;

· либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ [1].

Необходимо подчеркнуть, что линейные коэффициенты автокорреляции характеризуют тесноту только линейной связи текущего и предыдущих уровней ряда. Поэтому, по коэффициентам автокорреляции можно судить только о наличии или отсутствии линейной зависимости (или близкой к линейной). Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к 0 [2].