Экспериментальная оценка характеристик случайных сигналов

В экспериментальных исследованиях характеристики случайных процессов получают усреднением по времени. Эту операцию обозначим через <·>. Оценка математического ожидания процесса по j-й реализации длительностью Т будет

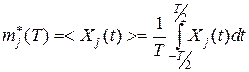(51)

Оценка корреляционной функции будет

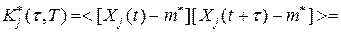
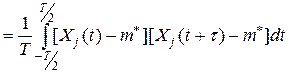(52)

Звездочка указывает, что оценки - случайные величины, зависящие от номера выбранной реализации j и длительности интервала наблюдения Т.

1.5.3. Эргодичность сигналов.

Стационарные случайные процессы (процессы, вероятностные характеристики которых не зависят от времени t и зависят только от интервала t₂-t₁), у которых средние по времени совпадают со средними по множеству, называют эргодическими, а такое свойство процессов - эргодичностью. Например, для эргодических процессов при любом j с вероятностью единица выполняются условия

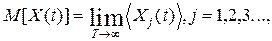(53)

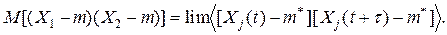
Эргодичность процессов имеет важное значение потому, что наблюдение за большим числом реализаций случайного процесса можно заменить наблюдением за одной, по достаточно продолжительной реализацией. Полученные таким образом характеристики процесса (математическое ожидание, дисперсия, корреляционная функция, спектральная плотность и др.) будут с достаточной точностью совпадать с теми, которые получают путем обработки большого числа реализаций.

1.5.4. Преобразования Хинчина - Винера.

Корреляционные и спектральные характеристики случайного процесса связаны соотношениями Хинчина - Винера:

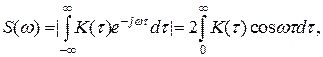(54)

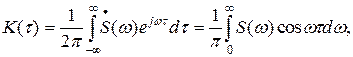(55)

где 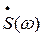- спектральная плотность случайного процессе.

Эти соотношения являются преобразованиями Фурье для случайных процессов. Особенность их в том, что в интегралах фигурируют не процессы, а их корреляционные функции. Из (54), (55) следует, что дисперсия процесса

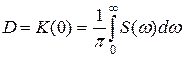(56)

Интегральной характеристикой спектральной плотности процесса служит ширина спектра

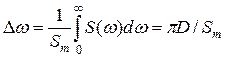, (57)

где 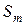- максимальное значение 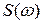. Интеграл (57) - это основание прямоугольника с высотой 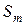, площадь которого равна площади под кривой .

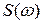1.5.5. Взаимно - корреляционные функции и взаимные спектральные плотности сигналов используют наряду с корреляционной функцией и спектральной плотностью. Взаимно - корреляционная функция двух процессов X₁(t) и X₂(t)

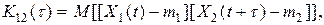(58)

где m₁ и m₂ - математические ожидания этих процессов.

Взаимная спектральная плотность

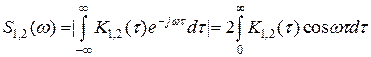(59)

Если взаимные характеристики полученные усреднением по множеству, совпадают с таковыми, полученными усреднением по времени, то процессы называют совместно - эргoдическими.