В качестве показателей эффективности СМО с ожиданием, кроме уже известных показателей — абсолютной А и относительной Q пропускной способности, вероятности отказа Pотк., среднего числа занятых каналов 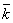 (для многоканальной системы) будем рассматривать также следующие: Lсист. - среднее число заявок системе; Тсист. — среднее время пребывания заявки в системе; Lоч. — среднее число заявок в очереди (длина очереди); Точ. — среднее время пребывания заявки в очереди; Рзан.. — вероятность того, что канал занят (степень загрузки канала).
(для многоканальной системы) будем рассматривать также следующие: Lсист. - среднее число заявок системе; Тсист. — среднее время пребывания заявки в системе; Lоч. — среднее число заявок в очереди (длина очереди); Точ. — среднее время пребывания заявки в очереди; Рзан.. — вероятность того, что канал занят (степень загрузки канала).
Одноканальная система с неограниченной очередью. На практике часто встречаются одноканальные СМО с неограниченной очередью (например, телефон-автомат с одной будкой).
Рассмотрим задачу.
Имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживании — интенсивность μ. Необходимо найти предельные вероятности состояний и показатели эффективности СМО.
Система может находиться в одном из состояний S0, S1, S2, …, Sk,по числу заявок, находящихся в СМО: S0 — канал свободен; S1 — канал занят (обслуживает заявку), очереди нет, S2 — канал занят, одна заявка стоит в очереди;... Sk — канал занят, (k—1)заявок стоят в очереди и т.д.
Граф состояний СМО представлен на рис. 8.

Рис. 8
Это процесс гибели и размножения, но с бесконечным числом состояний, в котором интенсивность потока заявок равна λ, а интенсивность потока обслуживании μ.
Прежде чем записать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время t→∞, очередь может неограниченно возрастать. Доказано, что если ρ<1, т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ≥1, очередь растет до бесконечности.
Для определения предельных вероятностей состояний воспользуемся формулами (16), (17) для процесса гибели и размножении (здесь мы допускаем известную нестрогость, так как ранее эти формулы были получены для случая конечного числа состояний системы). Получим 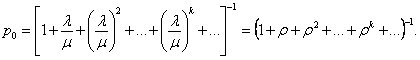 (32)
(32)
где, ρ = λ/μ
Так как предельные вероятности существуют лишь при ρ < 1, то геометрический ряд со знаменателем
ρ < 1, записанный в скобках в формуле (32), сходится к сумме, равной 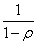 . Поэтому
. Поэтому
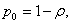 (33)
(33)
и с учетом соотношений (17)
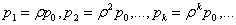
найдем предельные вероятности других состояний
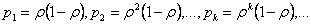 (34)
(34)
Предельные вероятности p0, p1, p2, …, pk,… образуют убывающую геометрическую профессию со знаменателем ρ < 1, следовательно, вероятность р0 — наибольшая. Это означает, что если СМО справляется с потоком заявок (при ρ < 1), то наиболее вероятным будет отсутствие заявок в системе.
Среднее число заявок в системе Lсист. определим по формуле математического ожидания, которая с учетом (34) примет вид
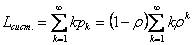 (35)
(35)
(суммирование от 1 до ∞, так как нулевой член 0p0=0).
Можно показать, что формула (35) преобразуется (при ρ < 1) к виду
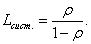 (36)
(36)
Найдем среднее число заявок в очереди Lоч. Очевидно, что
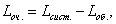 (37)
(37)
где Lоб. — среднее число заявок, находящихся под обслуживанием.
Среднее число заявок под обслуживанием определим по формуле математического ожидания числа заявок под обслуживанием, принимающего значения 0 (если канал свободен) либо 1 (если канал занят):
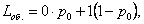
т.е. среднее число заявок под обслуживанием равно вероятности того, что канал занят:
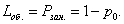 (38)
(38)
В силу (33)
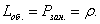 (39)
(39)
Теперь по формуле (37) с учетом (36) и (39)
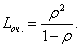 (40)
(40)
Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (в очереди), деленному на интенсивность потока заявок, т.е.
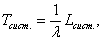 (41)
(41)
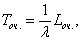 (42)
(42)
Формулы (41) и (42) называются формулами Литтла. Они вытекают из того, что в предельном, стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих ее: оба потока заявок имеют одну и ту же интенсивность λ.
На основании формул (41) и (42) с учетом (36) и (40) среднее время пребывания заявки в системе определится по формуле:
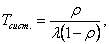 (43)
(43)
а среднее время пребывания заявки в очереди
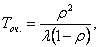 (44)
(44)
Многоканальная СМО с неограниченной очередью. Рассмотрим задачу. Имеется n-канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживании — интенсивность μ. Необходимо найти предельные вероятности состояний СМО и показатели ее эффективности.
Система может находиться в одном из состояний S0, S1, S2,…, Sk,…, Sn,…,— нумеруемых по числу заявок, находящихся в СМО: S0 — в системе нет заявок (все каналы свободны); S1 — занят один канал, остальные свободны; S2— заняты два канала, остальные свободны;..., Sk — занято k каналов, остальные свободны;..., Sn— заняты все n каналов (очереди нет); Sn+1— заняты все n каналов, в очереди одна заявка;..., Sn+r— заняты все n каналов, r заявок стоит в очереди,....
Граф состояний системы показан на рис. 9. Обратим внимание на то, что в отличие от предыдущей СМО, интенсивность потока обслуживаний (переводящего систему из одного состояния в другое справа налево) не остается постоянной, а по мере увеличения числа заявок в СМО от 0 до n увеличивается от величины m до nm, так как соответственно увеличивается число каналов обслуживания. При числе заявок в СМО большем, чем n, интенсивность потока обслуживании сохраняется равной nm.
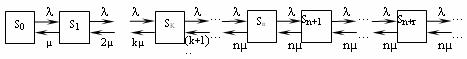
Рис. 9
Можно показать, что при r/n < 1 предельные вероятности существуют. Если r/n ≥ 1, очередь растет до бесконечности. Используя формулы (16) и (17) для процесса гибели и размножения, можно получить следующие формулы для предельных вероятностей состояний n-канальной СМО с неограниченной очередью
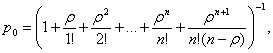 (45)
(45)
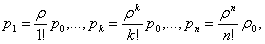 (46)
(46)
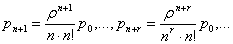 (47)
(47)
Вероятность того, что заявка окажется в очереди,
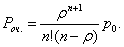 (48)
(48)
Для n-канальной СМО с неограниченной очередью, используя прежние приемы, можно найти:
среднее число занятых каналов
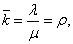 (49)
(49)
среднее число заявок в очереди
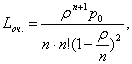 (50)
(50)
среднее число заявок в системе
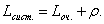 (51)
(51)
Среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе, как и ранее, находятся по формулам Литтла (42) и (41).
Замечание. Для СМО с неограниченной очередью при r < 1 любая заявка, пришедшая в систему, будет обслужена, т.е. вероятность отказа Pотк = 0, относительная пропускная способность Q = 1, а абсолютная пропускная способность равна интенсивности входящего потока заявок, т.е. А = l.
 2015-05-06
2015-05-06 984
984








