СТЕРЖЕНЬ
 Стержень массой М - материальный прямолинейный отрезок АВ длиной l. Вычислим момент инерции этого стержня относительно оси Аy
Стержень массой М - материальный прямолинейный отрезок АВ длиной l. Вычислим момент инерции этого стержня относительно оси Аy 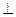 АВ. Разобьем стержень на бесконечно малые отрезки
АВ. Разобьем стержень на бесконечно малые отрезки 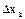 . Расстояние от
. Расстояние от 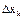 до точки А обозначим
до точки А обозначим 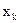 , а его массу -
, а его массу - 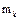 .
.
Тогда: 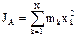 .
.
Линейная плотность стержня: 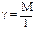 (кг/м). Масса
(кг/м). Масса 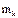 элементарного отрезка
элементарного отрезка 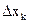 равна:
равна: 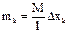 . Стержень однородный, тогда:
. Стержень однородный, тогда: 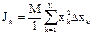 . Предел этой суммы - определённый интеграл по х в пределах от 0 до l:
. Предел этой суммы - определённый интеграл по х в пределах от 0 до l: 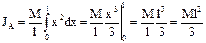 .
.
Момент инерции стержня относительно центра масс С вычисляется аналогично. Пределы в этом случае надо брать от 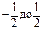 . В результате:
. В результате: 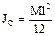 .
.
ПРЯМОУГОЛЬНИК
 Тонкая однородная пластина ОАВС со сторонами а и b и массой М. Вычислим момент инерции относительно оси y (стороны ОА). Разобьем площадь ОАВС прямыми, параллельными оси х, на бесконечно узкие полоски. Масса полоски -
Тонкая однородная пластина ОАВС со сторонами а и b и массой М. Вычислим момент инерции относительно оси y (стороны ОА). Разобьем площадь ОАВС прямыми, параллельными оси х, на бесконечно узкие полоски. Масса полоски - 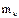 . Каждая полоска является прямолинейным отрезком, момент инерции которого:
. Каждая полоска является прямолинейным отрезком, момент инерции которого: 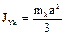 .
.
Момент инерции всего прямоугольника: 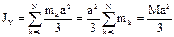 .
.
Аналогично относительно оси х: 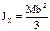 . Для момента инерции ОАВС относительно вершины О на основании связи полярного и осевых моментов, имеем:
. Для момента инерции ОАВС относительно вершины О на основании связи полярного и осевых моментов, имеем: 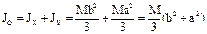 .
.
 2015-05-06
2015-05-06 945
945








