 КРУГ
КРУГ
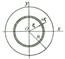
Вычислим момент инерции круга радиусом R и массой М относительно его центра О. Разобьем круг концентрическими окружностями на элементарные плоские кольца. Радиус такого кольца обозначим через 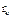 , его бесконечно малую ширину через
, его бесконечно малую ширину через 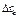 , а массу
, а массу 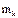 . Элементарное кольцо - материальную окружность, найдём ее момент инерции. Разобьем, всю окружность на бесконечно малые элементы - дуги. Массу элемента обозначим через
. Элементарное кольцо - материальную окружность, найдём ее момент инерции. Разобьем, всю окружность на бесконечно малые элементы - дуги. Массу элемента обозначим через 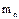 . Все элементы находятся от точки О на одном расстоянии
. Все элементы находятся от точки О на одном расстоянии 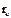 . Поэтому момент инерции такого кольца равен:
. Поэтому момент инерции такого кольца равен: 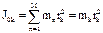 . Поверхностная плотность однородного круга:
. Поверхностная плотность однородного круга: 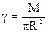 (кг/м2).
(кг/м2).
Масса элементарного кольца: 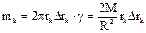 . Момент инерции круга равен:
. Момент инерции круга равен: 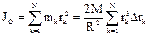 . Предел этой суммы - определённый интеграл по переменной r в пределах от 0 до R:
. Предел этой суммы - определённый интеграл по переменной r в пределах от 0 до R: 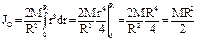 .
.
Моменты инерции круга относительно осей Ох и Oy: воспользуемся формулой, связывающей осевые моменты инерции с полярным, и учтём что осевые моменты инерции круга в силу симметрии равны между собой. Получаем: 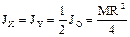 .
.
КРУГЛЫЙ ЦИЛИНДР
Вычислим момент инерции круглого цилиндра относительно его оси вращения z. Радиус основания цилиндра R, а его масса - M. Разобьем цилиндр плоскостями, параллельными его основанию, на бесконечно тонкие круглые пластики, масса которых 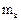 . Момент инерции такой пластинки относительно оси вращения цилиндра:
. Момент инерции такой пластинки относительно оси вращения цилиндра: 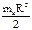 .
.
Момент инерции цилиндра: 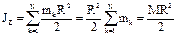 .
.
 2015-05-06
2015-05-06 841
841







