Сформулировать и доказать теорему о количестве движения точки в различных формах

Материальная точка массой m, движется относительно системы координат Oxyz под действием силы 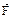. ДУ ее движения: 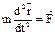или 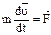. Т.к. масса постоянна: 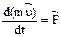(1): производная по времени от количества движения равна равнодействующей всех действующих на точку сил.

Умножим (1) на dt: 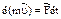(2): дифференциал количества движения точки равен элементарному импульсу всех действующий на точку сил.

Точка в момент t = 0 находилась в М₀ и имела скорость 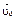, в момент t приходит в М и имеет скорость 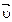. Проинтегрируем обе части (2): 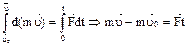: изменение количества движения точки за некоторый промежуток времени равно полному импульсу всех действующих на точку сил за тот же промежуток времени.